题目内容
【题目】已知方程
在
上有两个不等的实数根，则实数
的取值范围为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
由于
恒成立，构造函数
，则方程
在
上有两个不等的实数根等价于函数在上有两个不同的零点，利用导数研究函数在的值域即可解决问题。
由于恒成立，构造函数，则方程在上有两个不等的实数根等价于函数在上有两个不同的零点，
则
，
（1）当
时，则
在上恒成立，即函数
在上单调递增，
当
时，
，
，根据零点定理可得只有唯一零点，不满足题意；
（2）当
时，令，解得：
，令
，解得：
或
，
故的单调增区间为
，的单调减区间为
，
①当
，即
时，则在单调递增，当时，，，根据零点定理可得只有唯一零点，不满足题意；
②当
，即
时，则在上单调递增，在
上单调递减，
所以当时，，
，
，
故要使函数在上有两个不同的零点，
则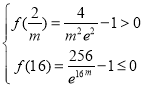
，解得：
；
综上所述：方程在上有两个不等的实数根，则实数
的取值范围为：
故答案选C
53天天练系列答案
【题目】大型综艺节目《最强大脑》中，有一个游戏叫做盲拧魔方，就是玩家先观察魔方状态并进行记忆，记住后蒙住眼睛快速还原魔方．根据调查显示，是否喜欢盲拧魔方与性别有关．为了验证这个结论，某兴趣小组随机抽取了100名魔方爱好者进行调查，得到的部分数据如表所示：已知在全部100人中随机抽取1人抽到喜欢盲拧的概率为
．
喜欢盲拧 | 不喜欢盲拧 | 总计 | |
男 | 10 | ||
女 | 20 | ||
总计 | 100 |
表（1）
并邀请这100人中的喜欢盲拧的人参加盲拧三阶魔方比赛，其完成时间的频率分布如表所示：
完成时间（分钟） | [0，10） | [10，20） | [20，30） | [30，40] |
频率 | 0.2 | 0.4 | 0.3 | 0.1 |
表（2）
（Ⅰ）将表（1）补充完整，并判断能否在犯错误的概率不超过0.001的前提下认为是否喜欢盲拧与性别有关？
（Ⅱ）现从表（2）中完成时间在[30，40] 内的人中任意抽取2人对他们的盲拧情况进行视频记录，记完成时间在[30，40]内的甲、乙、丙3人中恰有一人被抽到为事件A，求事件A发生的概率．
（参考公式：
，其中
）
P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
