题目内容
(18分)已知数列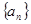 、
、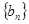 、
、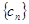 ,点
,点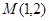 ,
,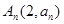 ,
,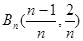 在一直线上。
在一直线上。
(1)求数列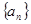 的通项公式;
的通项公式;
(2)若数列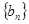 满足
满足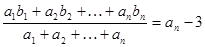 ,求数列
,求数列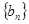 的通项公式;
的通项公式;
(3)若数列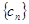 的前
的前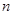 项和为
项和为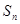 ,且满足
,且满足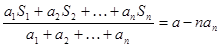 (
(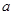 为常数),问点
为常数),问点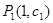 ,
,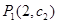 ,
, ,
,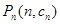 是否在同一直线上,请说明理由。
是否在同一直线上,请说明理由。
(1)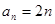 (2)
(2)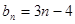 (3)求出
(3)求出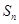 可以判断,当
可以判断,当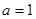 时,点
时,点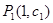 ,
,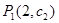 ,
,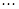 ,
,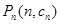 在同一直线上;当
在同一直线上;当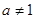 时,,点
时,,点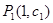 ,
,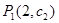 ,
,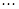 ,
,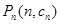 不在同一直线上
不在同一直线上
【解析】
试题分析:(1)由已知得: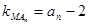 , ……2分
, ……2分
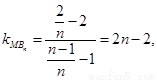 ……4分
……4分
又因为点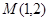 ,
,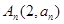 ,
,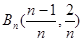 在一直线上,
在一直线上,
所以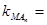
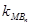 因此
因此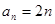 . ……6分
. ……6分
(2)由(1)得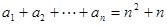 , ……8分
, ……8分
所以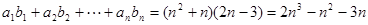 ,
,
当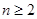 时,
时,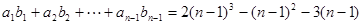 ,
,
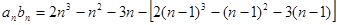
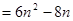 ,
,
所以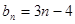 , ……10分
, ……10分
当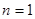 时,
时,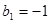 符合上式, ……11分
符合上式, ……11分
综上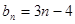 . ……12分
. ……12分
(3)由已知得: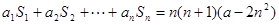 ,
,
当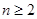 时,
时,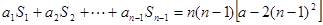 ,
,
所以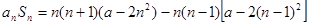 ,
,
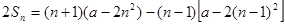
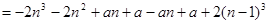
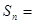
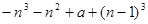
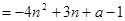 ,
,
当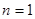 时,
时,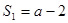 符合上式,
符合上式,
故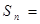
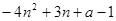 , ……16分
, ……16分
当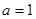 时,
时,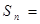
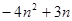 ,
,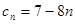 ,
,
此时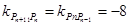 ,点
,点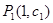 ,
,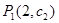 ,
,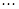 ,
,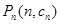 在同一直线上。
在同一直线上。
当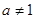 时,
时,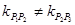 ,
,
所以点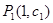 ,
,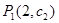 ,
,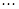 ,
,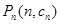 不在同一直线上。 ……18分
不在同一直线上。 ……18分
考点:本小题主要考查三点共线的应用、由递推关系式求数列的通项公式和数列的前n项和的求法等问题,考查学生对问题的理解能力和转化能力以及运算求解能力.
点评:解决数列问题时,出现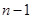 必须写上
必须写上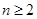 ,而且不能忘记验证
,而且不能忘记验证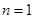 时是否满足要求.
时是否满足要求.
