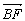题目内容
如下图，
PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠BAC=20°，求∠P的度数．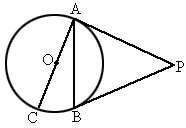
答案：略
解析：
提示：
解析：
|
解： ∠P=180°－∠PAB－∠PBA=180°－70°－70°=40°． |
提示：
|
分析：PA是⊙O切线，由切线垂直于过切点的半径，知∠CAP=90°，结合∠CAB=20°，可知∠PAB=70°，而又根据切线长的性质知PA=PB，所以∠PAB=∠PBA．这样，∠P的度数就容易求出了． |
练习册系列答案
相关题目
=1(a＞0,b＞0),A、B为其左、右两个顶点,P是双曲线C1上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.
时,求e2的取值范围.