Question

如下图，在底面是菱形的四棱锥P—ABCD中，∠ABC=60°,PA=AC=a,PB=PD=2a,点E在PD上，且PE∶ED=2∶1.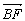

(1)证明:PA⊥平面ABCD；

(2)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.

Answer 1

证明：(1)∵底面ABCD是菱形,∠ABC=60°,?

∴AB=AD=AC=a.?

在△PAB中,由PA²+AB²=2a²=PB²,?

可知PA⊥AB,?

同理PA⊥AD,?

∵AB∩AD=A,?

∴PA⊥平面ABCD.?

(2)当F是棱PC的中点时,BF∥平面AEC,证明如下.?

证法一:取PE的中点M,连结FM,则?

FM∥CE.                       ①?

由EM=PE=ED,知E是MD的中点.?

连结BM、BD，设BD∩AC=O，则O为BD的中点.?

所以BM∥OE.                  ②?

由①②知，平面BFM∥平面AEC.?

又BF 平面BFM,所以BF∥平面AEC.?

证法二:因为=+=+(+)?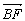

=++?

=+(-)+(-)?

=-,?

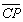所以、、共面.?

又BF 平面AEC,从而BF∥平面AEC.