题目内容
下列命题是真命题的有( )个
(1)?x∈(-∞,0),2x<3x
(2)若b2=ac,则a,b,c成等比数列;
(3)当x>0且x≠1时,有lnx+
≥2;
(4)若函数f(x)=ex,则?x1,x2∈R,都有f(
)≤
.
(1)?x∈(-∞,0),2x<3x
(2)若b2=ac,则a,b,c成等比数列;
(3)当x>0且x≠1时,有lnx+
| 1 |
| lnx |
(4)若函数f(x)=ex,则?x1,x2∈R,都有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
分析:根据指数函数的图象和性质,可以判断(1)的真假;根据等比数列的定义(各项均不为0),可判断(2)的真假;根据对数函数的图象和性质及对勾函数的图象和性质,可以判断(3)的真假;根据凹函数的图象和性质,及指数函数的图象和性质,可以判断(4)的真假.
解答:解:当x∈(-∞,0)时,2x>3x恒成立,故(1)错误;
若b2=ac=0,则a,b,c不能构成等比数列,故(2)错误;
当x>0且x≠1时,有lnx+
≥2或lnx+
≤2,故(3)错误;
函数f(x)=ex为凹函数,故?x1,x2∈R,都有f(
)≤
,故(4)正确
故选B
若b2=ac=0,则a,b,c不能构成等比数列,故(2)错误;
当x>0且x≠1时,有lnx+
| 1 |
| lnx |
| 1 |
| lnx |
函数f(x)=ex为凹函数,故?x1,x2∈R,都有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故选B
点评:本题以命题的真假判断为载体考查了指数函数的图象和性质,对数函数的图象和性质,凹函数的图象和性质,对勾函数的图象和性质,是函数图象和性质的一个简单综合应用.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 ,对
,对 都有
都有 ,则
,则 为偶函数
为偶函数 ,若对
,若对 ,都有
,都有 ,则函数
,则函数 中心对称
中心对称 与
与 是奇函数
是奇函数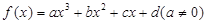 的图形一定是对称中心在图像上的中心对称图形。
的图形一定是对称中心在图像上的中心对称图形。 有两不同极值点
有两不同极值点 ,若
,若 ,且
,且 ,则关于的方程
,则关于的方程 的不同实根个数必有三个.
的不同实根个数必有三个.