题目内容
4．不等式log0.3（x2-3x-4）-log0.3（2x+10）＞0的解集是（ ）| A． | （-2，-1） | B． | （4，7） | C． | （-2，-1）∪（4，7） | D． | ∅ |
分析 要解的不等式即不等式log0.3（x2-3x-4）＞log0.3（2x+10），故0＜x2-3x-4＜2x+10，由此求得x的范围．
解答 解：不等式log0.3（x2-3x-4）-log0.3（2x+10）＞0，即 不等式log0.3（x2-3x-4）＞log0.3（2x+10），
故0＜x2-3x-4＜2x+10，求得-2＜x＜-1，或 4＜x＜7，
故选：C．
点评 本题主要考查对数函数的单调性和特殊点，对数函数的定义域，属于基础题．
练习册系列答案
天天向上口算本系列答案
相关题目
14．已知x、y满足y=3-$\sqrt{4x-{x}^{2}}$，则使x+2y+2a＜0恒成立的a的取值范围是（ ）
| A． | [$\sqrt{5}-4$，$\sqrt{5}+4$] | B． | （-∞，-5] | C． | [-5，+∞） | D． | （-∞，-5） |
15．函数y=lg（x-1）+lg（x-2）的定义域为M，函数y=lg（x2-3x+2）的定义域为N，则 （ ）
| A． | M?N | B． | N?M | C． | M=N | D． | M∩N=∅ |
12．若抛物线y=2x2上两点A（x1，y1）、B（x2，y2）关于直线y=x+$\frac{3}{2}$对称，则x1•x2=（ ）
| A． | $\frac{5}{2}$ | B． | 2 | C． | -$\frac{1}{2}$ | D． | -3 |
19．已知集合A={x|lg（x-1）＜1}，B={x|$\frac{x+2}{4-x}$≥0}，则A∩B=（ ）
| A． | {x|-2≤x≤4} | B． | {x|4＜x＜11} | C． | {x|1＜x＜4} | D． | {x|-2≤x＜4} |
9．在等比数列{an}中，Sn是其前n项和，已知a3=2S2+1，a4=2S3+1，则S4=（ ）
| A． | 4 | B． | 16 | C． | 20 | D． | 40 |
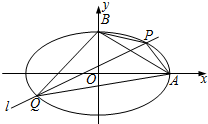已知平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点和上顶点分别为A，B，椭圆的离心率为$\frac{\sqrt{3}}{2}$，且过点（1，$\frac{\sqrt{3}}{2}$）．