题目内容
已知函数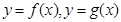 的导函数的图像如下图,那么
的导函数的图像如下图,那么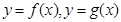 的图像可能是( )
的图像可能是( )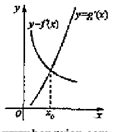

D
解析试题分析:从函数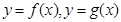 的导函数的图像上看,
的导函数的图像上看, 时,
时, 且
且 单调递减;
单调递减; 且
且 单调递增,所以函数
单调递增,所以函数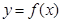 在
在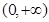 单调递增且在该曲线上的点的切线的斜率越来越小,其图像特征为“逐渐上升且上凸”,而函数
单调递增且在该曲线上的点的切线的斜率越来越小,其图像特征为“逐渐上升且上凸”,而函数 在
在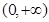 单调递增且在该曲线上的点的切线的斜率越来越大,其图像特征为“逐渐上升且下凸”,符合这一特征的只有B、D,而从导函数的图像上看,在
单调递增且在该曲线上的点的切线的斜率越来越大,其图像特征为“逐渐上升且下凸”,符合这一特征的只有B、D,而从导函数的图像上看,在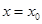 处,两函数的导数值相等即两曲线在该点处的切线的斜率相等,故只能选D.
处,两函数的导数值相等即两曲线在该点处的切线的斜率相等,故只能选D.
考点:1.函数的单调性与导数;2.导数的几何意义.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
设函数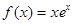 ,则( )
,则( )
A.x=1为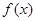 的极大值点 的极大值点 |
B.x=-1为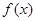 的极大值点 的极大值点 |
C.x=1为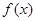 的极小值点 的极小值点 |
D.x=-1为 的极小值点 的极小值点 |
若 ,则
,则 等于( )
等于( )
| A.-1 | B.-2 | C.1 | D. |
设函数
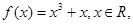 若当0
若当0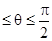 时,
时,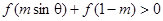 恒成立,则实数m的取值范围是 ( )
恒成立,则实数m的取值范围是 ( )
| A.(0,1) | B.(-∞,0) | C.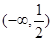 | D.(-∞,1) |
已知函数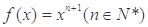 的图象与直线
的图象与直线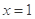 交于点P,若图象在点P处的切线与x轴交点的横坐标为
交于点P,若图象在点P处的切线与x轴交点的横坐标为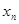 ,则
,则 +
+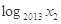 +…+
+…+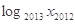 的值为( )
的值为( )
| A.-1 | B.1-log20132012 | C.-log20132012 | D.1 |
函数f(x)=ax3-x在R上为减函数,则( )
| A.a≤0 | B.a<1 | C.a<0 | D.a≤1 |
若 则
则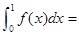 ( )
( )
A.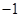 | B. | C.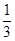 | D.1 |
设f(x),g(x)在[a,b]上可导,且f′(x)>g′(x),则当a<x<b时,有( )
| A.f(x)>g(x) |
| B.f(x)<g(x) |
| C.f(x)+g(a)>g(x)+f(a) |
| D.f(x)+g(b)>g(x)+f(b) |
三次函数f(x)=mx3-x在(-∞,+∞)上是减函数,则m的取值范围是 ( )
| A.m<0 | B.m<1 | C.m≤0 | D.m≤1 |