题目内容
当x＞0时，函数y=（a2-1）x的值总大于1，则实数a的取值范围是
- A.
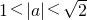
- B.|a|＜1
- C.|a|＞1
- D.
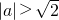
D
分析：根据题意指数函数y=ax的图象与性质得出关于底数的不等关系，再解此不等式即可求得实数a的取值范围．
解答：∵当x＞0时，函数y=（a2-1）x的值总大于1，
根据指数函数的性质得：
a2-1＞1，
∴a2＞2，
则实数a的取值范围是．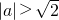
故选D．
点评：本题主要考查指数函数的图象与性质、不等式的解法．属于容易题．
分析：根据题意指数函数y=ax的图象与性质得出关于底数的不等关系，再解此不等式即可求得实数a的取值范围．
解答：∵当x＞0时，函数y=（a2-1）x的值总大于1，
根据指数函数的性质得：
a2-1＞1，
∴a2＞2，
则实数a的取值范围是
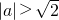．故选D．
点评：本题主要考查指数函数的图象与性质、不等式的解法．属于容易题．
练习册系列答案
相关题目
当x＞0时，函数y=（a2-1）x的值总大于1，则实数a的取值范围是（ ）
A、1＜|a|＜
| ||
| B、|a|＜1 | ||
| C、|a|＞1 | ||
D、|a|＞
|
已知幂函数y=f（x）的图象经过点（2，4），对于偶函数y=g（x）（x∈R），当x≥0时，g（x）=f（x）-2x．已知函数f（x）=
在x=1取得极值2，则当x＞0时，函数y=
（ ）
| ax |
| x2+b |
| x2+a |
| bx |
| A、有最小值2 |
| B、有最大值2 |
| C、有最小值4 |
| D、有最大值4 |