题目内容
19.设等差数列{an}的前n项为Sn,已知a1=-11,a3+a7=-6,当Sn取最小值时,n=6.分析 由已知条件利用等差数列通项公式求出公差d=2,再由等差数列的前n项和公式求出Sn,利用配方法能求出当Sn取最小值时n的值.
解答 解:∵等差数列{an}的前n项为Sn,
a1=-11,a3+a7=-6,
∴-11+2d-11+6d=-6,解得d=2,
∴Sn=-11n+$\frac{n(n-1)}{2}×2$=n2-12n=(n-6)2-36,
∴当Sn取最小值-36时,n=6.
故答案为:6.
点评 本题考查等差数列的前n项和取最小值时项数n的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.曲线f(x)=x3+$\sqrt{x}$在点(1,2)处的切线方程为( )
| A. | 4x-y-2=0 | B. | 7x-2y-3=0 | C. | 3x-y-1=0 | D. | 5x-y-3=0 |
4.给出下列四种说法:
(1)函数y=ax(a>0且a≠1)与函数$y={log_a}{a^x}(a>0$且a≠1)的定义域相同;
(2)函数y=x2与函数y=3x的值域相同;
(3)函数$y=\frac{1}{2}+\frac{1}{{{2^x}-1}}$与函数$y=\frac{{{{(1+{2^x})}^2}}}{{x•{2^x}}}$均是定义在(-∞,0)∪(0,+∞)上的奇函数;
(4)函数y=(x-1)2与函数y=2x-1在(0,+∞)上都是奇函数.
其中正确说法的序号是( )
(1)函数y=ax(a>0且a≠1)与函数$y={log_a}{a^x}(a>0$且a≠1)的定义域相同;
(2)函数y=x2与函数y=3x的值域相同;
(3)函数$y=\frac{1}{2}+\frac{1}{{{2^x}-1}}$与函数$y=\frac{{{{(1+{2^x})}^2}}}{{x•{2^x}}}$均是定义在(-∞,0)∪(0,+∞)上的奇函数;
(4)函数y=(x-1)2与函数y=2x-1在(0,+∞)上都是奇函数.
其中正确说法的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (3)(4) |
11.已知函数f(x)是定义在(0,+∞)上的增函数,且对任意的x,y∈(0,+∞),都有f(x+y)=f(x)+f(y)-1,已知f(4)=5.
(Ⅰ)求f(2)的值;
(Ⅱ)解不等式f(m-2)≤2.
(Ⅰ)求f(2)的值;
(Ⅱ)解不等式f(m-2)≤2.
9.函数f(x)=$\sqrt{x}$-x的单调递减区间为( )
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{1}{4}$)∪$\frac{1}{2}$,+∞) | C. | ($\frac{1}{4}$,+∞) | D. | ($\frac{1}{2}$,+∞) |
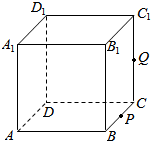 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是②④(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是②④(写出所有正确命题的编号).