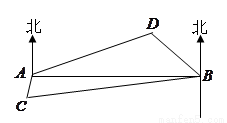题目内容
 如图,A,B是海面上位于东西方向相距5(3+
如图,A,B是海面上位于东西方向相距5(3+| 3 |
| 6 |
分析:在三角形ABD中,由AB,∠ADB,以及∠DAB的度数,利用正弦定理求出BD的长,连接CD,在三角形BCD中,由BC,BD,及∠CBD的度数,利用余弦定理求出CD的长,即为该救援船到达D点的路程,利用时间=路程÷速度,即可求出该救援船到达D点需要的时间.
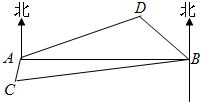
解答: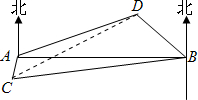 解:在△ABD中,AB=5(3+
解:在△ABD中,AB=5(3+
)海里,∠ADB=60°+45°=105°,
由正弦定理:
=
,
即
=
,
∴2BD=
,即BD=5
,
连接CD,在△CBD中,BC=15
,BD=5
,∠CBD=15°+45°=60°,
由余弦定理:CD2=BC2+BD2-2BC•BDcos60°=(15
)2+(5
)2-2×15
×5
cos60°=1350+150-450=1050,
∴CD=5
(海里),
∴t=
=
(小时).
答:该救援船到达D点需要的时间为
小时.
 解:在△ABD中,AB=5(3+
解:在△ABD中,AB=5(3+| 3 |
由正弦定理:
| AB |
| sin∠ADB |
| BD |
| sin30° |
即
5(3+
| ||
| sin(60°+45°) |
| BD | ||
|
∴2BD=
20
| ||||
|
| 6 |
连接CD,在△CBD中,BC=15
| 6 |
| 6 |
由余弦定理:CD2=BC2+BD2-2BC•BDcos60°=(15
| 6 |
| 6 |
| 6 |
| 6 |
∴CD=5
| 42 |
∴t=
5
| ||
| 30 |
| ||
| 6 |
答:该救援船到达D点需要的时间为
| ||
| 6 |
点评:此题属于解三角形的题型,涉及的知识有:正弦、余弦定理,特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,A,B是海面上位于东西方向相距5(3+
如图,A,B是海面上位于东西方向相距5(3+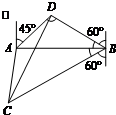 如图,A,B是海面上位于东西方向相距
如图,A,B是海面上位于东西方向相距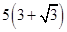 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距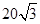 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?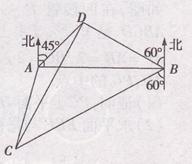
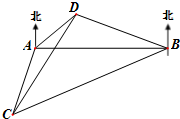
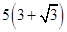 海里的两个观测点,现位于A点北偏东60°,B点北偏西45°的D点有一艘轮船发出求救信号,位于B点南偏西75°且与B点相距
海里的两个观测点,现位于A点北偏东60°,B点北偏西45°的D点有一艘轮船发出求救信号,位于B点南偏西75°且与B点相距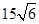 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?