题目内容
11．椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的离心率是（ ）| A． | $\frac{3}{4}$ | B． | $\frac{5}{\sqrt{41}}$ | C． | $\frac{4}{5}$ | D． | $\frac{3}{5}$ |
分析 先根据椭圆的标准方程得出：长轴长，短轴长，进而根据椭圆a，b，c的关系a2=b2+c2可表示出c，再由e=$\frac{c}{a}$得到答案
解答 解：∵椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1，
∴a=5，b=4
∴c=3
∴e=$\frac{c}{a}$=$\frac{3}{5}$
故选：D．
点评 本题主要考查椭圆的简单性质：椭圆离心率的计算，属基础题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
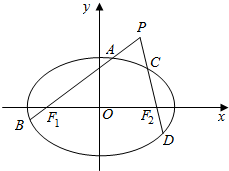如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为F1，F2，离心率为$\frac{{\sqrt{2}}}{2}$，它的四个顶点连成的菱形的面积为8$\sqrt{2}$．过动点P（不在x轴上）的直线PF1，PF2与椭圆的交点分别为A，B和C，D．
16．椭圆$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1的焦距为（ ）
| A． | 2 | B． | 3 | C． | 2$\sqrt{2}$ | D． | 4 |
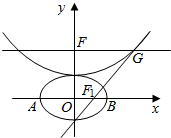设b＞0，椭圆方程为$\frac{{x}^{2}}{2{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1，抛物线方程为y=$\frac{1}{8}$x2+b，如图所示，过点F（0，b+2）作x轴的平行线，与抛物线在第一象限的焦点为G，已知抛物线在G点的切线经过椭圆的右焦点F1