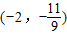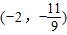题目内容
(Ⅰ)已知a+a-1=3,求a2+a-2的值;
(Ⅱ)化简求值:1.10+
-0.5-2+lg25+2lg2;
(Ⅲ)解不等式:log2(x+1)<1.
(Ⅱ)化简求值:1.10+
| 3 | 64 |
(Ⅲ)解不等式:log2(x+1)<1.
分析:(Ⅰ)把a+a-1=3两边平方,展开变形可得答案;
(Ⅱ)由指数和对数的运算性质,化简可得;
(Ⅲ)原不等式可化为log2(x+1)<log22,由对数函数的定义域和单调性可得关于x的不等式组,解不等式组可得.
(Ⅱ)由指数和对数的运算性质,化简可得;
(Ⅲ)原不等式可化为log2(x+1)<log22,由对数函数的定义域和单调性可得关于x的不等式组,解不等式组可得.
解答:解:(Ⅰ)∵a+a-1=3,∴(a+a-1)2=9,
展开可得a2+2+a-2=9,解得a2+a-2=7
(Ⅱ)原式1+4-4+2lg5+2lg2
=1+2(lg5+lg2)=1+2lg10
=1+2=3
(Ⅲ)原不等式可化为log2(x+1)<log22,
∴
,解得-1<x<1
∴不等式的解集为(-1,1)
展开可得a2+2+a-2=9,解得a2+a-2=7
(Ⅱ)原式1+4-4+2lg5+2lg2
=1+2(lg5+lg2)=1+2lg10
=1+2=3
(Ⅲ)原不等式可化为log2(x+1)<log22,
∴
|
∴不等式的解集为(-1,1)
点评:本题考查根式与指数幂的互化,涉及对数的性质,属基础题.

练习册系列答案
相关题目
选择题:
(1)
已知 ,
, ,
, ,则
,则
[
]|
(A)A 、B、D三点共线 |
(B)A 、B、C三点共线 |
|
(C)B 、C、D三点共线 |
(D)A 、C、D三点共线 |
(2)
已知正方形ABCD的边长为1, ,
, ,
, ,则
,则 等于
等于
[
]|
(A)0 |
(B)3 |
(C) |
(D) |
(3)
已知 ,
, ,
, ,
, ,且四边形ABCD为平行四边形,则
,且四边形ABCD为平行四边形,则
[
]|
(A)a +b+c+d=0 |
(B)a -b+c-d=0 |
|
(C)a +b-c-d=0 |
(D)a -b-c+d=0 |
(4)
已知D、E、F分别是△ABC的边BC、CA、AB的中点,且 ,
, ,
, ,则①
,则① ;②
;② ;③
;③ ;④
;④
中正确的等式的个数为
[
]|
(A)1 |
(B)2 |
(C)3 |
(D)4 |
(5)
若 ,
, 是夹角为60°的两个单位向量,则
是夹角为60°的两个单位向量,则 ;
; 的夹角为
的夹角为
[
]|
(A)30° |
(B)60° |
(C)120° |
(D)150° |
(6)
若向量a、b、c两两所成的角相等,且 ,
,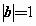 ,
, ,则
,则 等于
等于
[
]|
(A)2 |
(B)5 |
(C)2 或5 |
(D)  |
(7)
等边三角形ABC的边长为1, ,
, ,
, ,那么a·b+b·c+c·a等于
,那么a·b+b·c+c·a等于
[
]|
(A)3 |
(B) -3 |
(C) |
(D) |