题目内容
已知a≠b(a、b∈R)是关于x的方程x2-(k-1)x+k2=0两个根,则以下结论正确的是( )A.k的取值范围为(-1,3)
B.若a,b∈(-∞,0),则k的取值范围为(-∞,1)
C.ab+2(a+b)的取值范围是
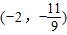
D.若a<-1<b,则k的取值范围为(-1,0)
【答案】分析:若方程有两个根,则△>0,解不等式可得k的取值范围;若a,b∈(-∞,0),则方程有两个负根,△>0且k-1<0;根据韦达定理可将ab+2(a+b)化为一个关于k的表达式,根据二次函数的图象和性质,可得其取值范围,若a<-1<b,则当x=-1时,x2-(k-1)x+k2<0,由此可得k的取值范围.
解答:解:∵a≠b(a、b∈R)是关于x的方程x2-(k-1)x+k2=0两个根,∴(k-1)2-4k2=-3k2-2k+1>0,即3k2+2k-1<0,解得-1<k< ,故A错误;
,故A错误;
若a,b∈(-∞,0),则k-1<0且-1<k< ,故k的取值范围为(-1,1),故B错误;
,故k的取值范围为(-1,1),故B错误;
ab+2(a+b)=k2+2(k-1)=k2+2k-2=(k+1)2-3,(-1<k< ),即ab+2(a+b)∈(-3,-
),即ab+2(a+b)∈(-3,-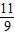 ),故C错误
),故C错误
若a<-1<b,当x=-1时,x2-(k-1)x+k2<0,即k+k2<0,解得k∈(-1,0),故D正确
故选D
点评:本题考查的知识点是根与系数的关系,其中熟练掌握一元二次方程根的个数与△的关系是解答本题的关键.
解答:解:∵a≠b(a、b∈R)是关于x的方程x2-(k-1)x+k2=0两个根,∴(k-1)2-4k2=-3k2-2k+1>0,即3k2+2k-1<0,解得-1<k<
 ,故A错误;
,故A错误;若a,b∈(-∞,0),则k-1<0且-1<k<
 ,故k的取值范围为(-1,1),故B错误;
,故k的取值范围为(-1,1),故B错误;ab+2(a+b)=k2+2(k-1)=k2+2k-2=(k+1)2-3,(-1<k<
 ),即ab+2(a+b)∈(-3,-
),即ab+2(a+b)∈(-3,-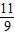 ),故C错误
),故C错误若a<-1<b,当x=-1时,x2-(k-1)x+k2<0,即k+k2<0,解得k∈(-1,0),故D正确
故选D
点评:本题考查的知识点是根与系数的关系,其中熟练掌握一元二次方程根的个数与△的关系是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目