题目内容
设函数![]() 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为f(x).
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为f(x).
(1)若方程f(x)=0有两个实根分别为-2和4,求f(x)的表达式;
(2)若g(x)在区间[-1,3]上是单调递减函数,求a2+b2的最小值.
答案:
解析:
解析:
|
(1)因为函数 根据导数的几何意义知 由已知-2、4是方程 由韦达定理, (2) 这只需满足 而 所以当 |

练习册系列答案
相关题目
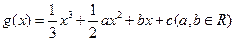 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为 .
.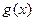 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求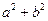 的最小值.
的最小值. 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为 .
. 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求 的最小值.
的最小值.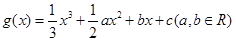 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为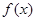 .
. 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求 的最小值.
的最小值.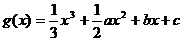
 的图象经过原点,在其图象上一点P
的图象经过原点,在其图象上一点P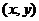 处的切线斜率记为
处的切线斜率记为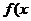 ).若方程
).若方程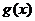 在区间
在区间 上是单调递减函数,则
上是单调递减函数,则 的最小值为________.
的最小值为________.