题目内容
设函数![]() 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为![]() .
.
(1)若方程![]() =0有两个实根分别为-2和4,求
=0有两个实根分别为-2和4,求![]() 的表达式;
的表达式;
(2)若![]() 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求![]() 的最小值.
的最小值.
【解析】(Ⅰ)因为函数![]() 的图象经过原点,所以
的图象经过原点,所以![]() ,则
,则![]() .
.
根据导数的几何意义知![]() ,………4分
,………4分
由已知—2、4是方程![]() 的两个实数,
的两个实数,
由韦达定理,![]() …………6分
…………6分
(Ⅱ)![]() 在区间[—1,3]上是单调减函数,所以在[—1,3]区间上恒有
在区间[—1,3]上是单调减函数,所以在[—1,3]区间上恒有
![]() ,即
,即![]() 在[—1,3]恒成立,
在[—1,3]恒成立,
这只需满足![]() 即可,也即
即可,也即![]() …………10分
…………10分
而![]() 可视为平面区域
可视为平面区域![]() 内的点到原点距离的平方,其中点(—2,—3)距离原点最近,
内的点到原点距离的平方,其中点(—2,—3)距离原点最近,
所以当![]() 时,
时, ![]() 有最小值13…………13分
有最小值13…………13分

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
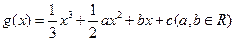 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为 .
.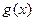 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求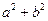 的最小值.
的最小值. 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为 .
. 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求 的最小值.
的最小值.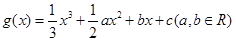 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为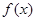 .
. 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求 的最小值.
的最小值.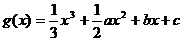
 的图象经过原点,在其图象上一点P
的图象经过原点,在其图象上一点P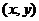 处的切线斜率记为
处的切线斜率记为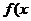 ).若方程
).若方程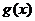 在区间
在区间 上是单调递减函数,则
上是单调递减函数,则 的最小值为________.
的最小值为________.