题目内容
已知偶函数y=f(x)=ax2+bx+c的最小值为-1,且f(1)=0.
(1)求该函数的表达式f(x).
(2)过曲线C:y=f(x)(x>0)上的点P作曲线C的切线,与x轴、y轴分别交于点M,N,试确定点P的坐标,使△MON的面积最小.
[求商的导数的法则是: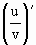 =
=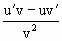 ]
]
答案:
解析:
解析:
|
解:(1)因为该函数为偶函数, 所以f(-x)=f(x)对定义域内一切x∈R正成立.所以f(-1)=f(1),所以b=0.因为f(1)=0,所以a+c=0,c=-a.所以f(x)=ax2-a.由此,当a>0时,f(x)有最小值-a.所以-a=-1,a=1,所以f(x)=x2-1. (2)如图所示,设切点为P(u,t),则t=u2-1.因为y=x2-1(x>0),所以
所以过P点的切线l的方程为y-t=2u(x-u).则切线l与x,y轴的交点分别为M( |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
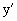 =2x,kt=2u.
=2x,kt=2u.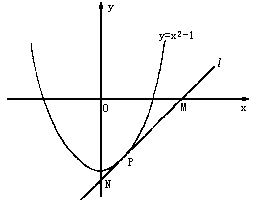
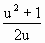 ,0),N(0,-u2-1).所以△MON的面积S=
,0),N(0,-u2-1).所以△MON的面积S=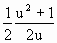 (u2+1)=
(u2+1)=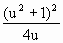 .所以
.所以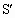 =
=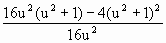 =
=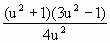 .令
.令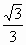 .因为u>0,所以u=
.因为u>0,所以u=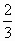 .所以,点P的坐标为(
.所以,点P的坐标为(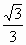 ,-
,-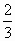 ).
).