题目内容
已知点(cosθ,sinθ)到直线xsinθ+ycosθ-1=0的距离是
(0≤θ≤
),则θ的值为( )
| 1 |
| 2 |
| π |
| 2 |
分析:由点到直线的距离公式可得|sin2θ|=
,由 0≤θ≤
,可得0≤2θ≤π,sin2θ≥0,故有 sin2θ=
,由此求得θ的值.
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
解答:解:由点到直线的距离公式可得点(cosθ,sinθ)到直线xsinθ+ycosθ-1=0的距离是
=|sin2θ|=
,
由 0≤θ≤
,可得0≤2θ≤π,sin2θ≥0,∴|sin2θ|=sin2θ.
故有 sin2θ=
,∴2θ=
,或 2θ=
,即 θ=
,或θ=
.
故选 C.
| |cosθsinθ+sinθcosθ| | ||
|
| 1 |
| 2 |
由 0≤θ≤
| π |
| 2 |
故有 sin2θ=
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 12 |
| 5π |
| 12 |
故选 C.
点评:本题主要考查点到直线的距离公式的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
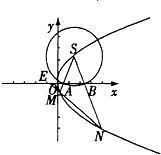 已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=
已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|= 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= .
.
 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;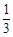 |NE|,求cos∠MSN的值.
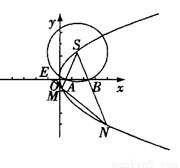
|NE|,求cos∠MSN的值. 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= .
. 
 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点; |NE|,求cos∠MSN的值.
|NE|,求cos∠MSN的值.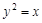 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|=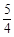 。
。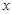 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;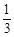 |NE|,求cos∠MSN的值。
|NE|,求cos∠MSN的值。