题目内容
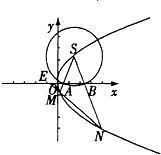 已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=
已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=| 5 |
| 4 |
(Ⅰ)求点S的坐标;
(Ⅱ)以S为圆心的动圆与x轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
①判断直线MN的斜率是否为定值,并说明理由;
②延长NM交x轴于点E,若|EM|=
| 1 |
| 3 |
分析:(Ⅰ)设S(x0,y0)(y0>0),由已知得F(
,0),则|SF|=x0+
=
,x0=1,由此能求出点S的坐标.
(Ⅱ)①设直线SA的方程为y-1=k(x-1)(k≠0),M(x1,y1),由
,得ky2-y+1-k=0,所以M(
,
-1).由已知SA=SB,知直线SB的斜率为-k,由此能导出直线MN的斜率为定值-
.
②设E(t,0),由|EM|=
|NE|,知k=2.所以直线SA的方程为y=2x-1,则A(
,0),同理B(
,0).由此能求出cos∠MSN的值.
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
(Ⅱ)①设直线SA的方程为y-1=k(x-1)(k≠0),M(x1,y1),由
|
| (1-k)2 |
| k2 |
| 1 |
| k |
| 1 |
| 2 |
②设E(t,0),由|EM|=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:(Ⅰ)设S(x0,y0)(y0>0),由已知得F(
,0),则|SF|=x0+
=
,x0=1,
∴y0=1,∴点S的坐标是(1,1)------------------------(2分)
(Ⅱ)①设直线SA的方程为y-1=k(x-1)(k≠0),M(x1,y1),
由
得ky2-y+1-k=0,
∴y1+1=
,y1=
-1,∴M(
,
-1).
由已知SA=SB,∴直线SB的斜率为-k,∴,
∴kMN=
=-
--------------(7分)
②设E(t,0),∵|EM|=
|NE|,∴
=
,
∴(
-t,
-1)=
(
-t,-
-1),则
-1=
(-
-1),∴k=2----------------(8分)
∴直线SA的方程为y=2x-1,则A(
,0),同理B(
,0)
∴cos∠MSN=cos∠ASB=
=
---------------------------(12分)
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
∴y0=1,∴点S的坐标是(1,1)------------------------(2分)
(Ⅱ)①设直线SA的方程为y-1=k(x-1)(k≠0),M(x1,y1),
由
|
∴y1+1=
| 1 |
| k |
| 1 |
| k |
| (1-k)2 |
| k2 |
| 1 |
| k |
由已知SA=SB,∴直线SB的斜率为-k,∴,
∴kMN=
| ||||
|
| 1 |
| 2 |
②设E(t,0),∵|EM|=
| 1 |
| 3 |
| EM |
| 1 |
| 3 |
| EN |
∴(
| (1-k)2 |
| k2 |
| 1 |
| k |
| 1 |
| 3 |
| (1+k)2 |
| k2 |
| 1 |
| k |
| 1 |
| k |
| 1 |
| 3 |
| 1 |
| k |
∴直线SA的方程为y=2x-1,则A(
| 1 |
| 2 |
| 3 |
| 2 |
∴cos∠MSN=cos∠ASB=
| SA2+SB2-AB2 |
| 2SA•SB |
| 3 |
| 5 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆锥曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= .
.
 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;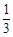 |NE|,求cos∠MSN的值.
|NE|,求cos∠MSN的值. 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= .
. 
 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点; |NE|,求cos∠MSN的值.
|NE|,求cos∠MSN的值. 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= 。
。 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点; |NE|,求cos∠MSN的值。
|NE|,求cos∠MSN的值。