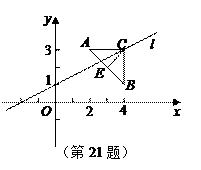题目内容
 如图,已知点A(
如图,已知点A(| 3 |
|
(1)以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,求圆C的极坐标方程;
(2)过原点O作直线l的垂线,垂足为H,若动点M0满足2
| OM |
| OH |
分析:(1)由条件求得圆的直角坐标方程为 (x-
)2+(y-
)2=1,由于OC和x轴的正方向的夹角为
,在圆上任意取一点M(ρ,θ),则 ρ=2•cos(θ-
)即为所求.
(2)由条件可得直线l的普通方程为xsinφ-ycosφ-cosφ=0,由于2
=3
,可得 M(
sin2φ,-
-
cos2φ),由此得到点M轨迹的参数方程.
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
(2)由条件可得直线l的普通方程为xsinφ-ycosφ-cosφ=0,由于2
| OM |
| OH |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:(1)∵点A(
,0),B(0,1),圆C是以AB为直径的圆,故点C的坐标为(
,
),半径等于
|AB|=1,
故圆的方程为 (x-
)2+(y-
)2=1. (2’)
由于OC和x轴的正方向的夹角为
,在圆上任意取一点M(ρ,θ),则 ρ=2•cos(θ-
),
故圆的极坐标方程为 ρ=2•cos(θ-
). (4’)
(2)直线l的普通方程为xsinφ-ycosφ-cosφ=0,(5’)
点 H(
sin2φ,-
-
cos2φ). (7’)
由于2
=3
,∴M(
sin2φ,-
-
cos2φ),(9’)
∴点M轨迹的参数方程为
,φ为参数,图形为圆. (10’)
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故圆的方程为 (x-
| ||
| 2 |
| 1 |
| 2 |

由于OC和x轴的正方向的夹角为
| π |
| 6 |
| π |
| 6 |
故圆的极坐标方程为 ρ=2•cos(θ-
| π |
| 6 |
(2)直线l的普通方程为xsinφ-ycosφ-cosφ=0,(5’)
点 H(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由于2
| OM |
| OH |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
∴点M轨迹的参数方程为
|
点评:本题主要考查把参数方程化为普通方程的方法,圆的参数方程,简单曲线的极坐标方程,属于基础题.

练习册系列答案
相关题目
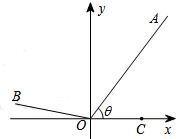 如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.
如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.