题目内容
若多项式(1+x)m=a0+a1x+a2x2+…+amxm满足:a1+2a2+3a3+…+mam=80,则 的值是
的值是
- A.

- B.

- C.

- D.

B
分析:y′=m(1+x)m-1=a1+2a2x+3a3x2+…+mamxm-1,令x=1,得2m-1m=a1+2a2+3a3+…+mam=80.解得m=5.所以 =
=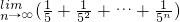 =
=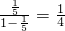 .
.
解答:设y=(1+x)m=a0+a1x+a2x2+…+amxm,
y′=m(1+x)m-1=a1+2a2x+3a3x2+…+mamxm-1,
令x=1,得2m-1m=a1+2a2+3a3+…+mam=80.
解得m=5.∴a4=C54=5.
∴ =
=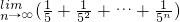
=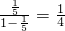 .
.
故选B.
点评:本题考查极限及其运算,解题的关键是利用导数求出m的值.
分析:y′=m(1+x)m-1=a1+2a2x+3a3x2+…+mamxm-1,令x=1,得2m-1m=a1+2a2+3a3+…+mam=80.解得m=5.所以
 =
=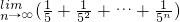 =
=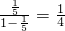 .
.解答:设y=(1+x)m=a0+a1x+a2x2+…+amxm,
y′=m(1+x)m-1=a1+2a2x+3a3x2+…+mamxm-1,
令x=1,得2m-1m=a1+2a2+3a3+…+mam=80.
解得m=5.∴a4=C54=5.
∴
 =
=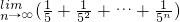
=
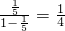 .
.故选B.
点评:本题考查极限及其运算,解题的关键是利用导数求出m的值.

练习册系列答案
相关题目
 的值是( )
的值是( )


