题目内容
已知函数f(x)=ax2+4x-2,若对任意x1,x2∈R且x1≠x2,都有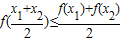 .
.(Ⅰ)求实数a的取值范围;
(Ⅱ)(理)对于给定的非零实数a,求最小的负数M(a),使得x∈[M(a),0]时,-4≤f(x)≤4都成立;
(Ⅲ)(理)在(Ⅱ)的条件下,当a为何值时,M(a)最小,并求出M(a)的最小值.
(Ⅱ)(文)求最小的实数b,使得x∈[b,1]时,f(x)≥-2都成立;
(Ⅲ)(文)若存在实数a,使得x∈[b,1]时,-2≤f(x)≤3b都成立,求实数b的取值范围.
【答案】分析:(I)由已知中函数f(x)=ax2+4x-2,我们求出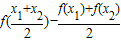 的解析式,并根据
的解析式,并根据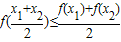 判断其符号,即可得到实数a的取值范围;
判断其符号,即可得到实数a的取值范围;
(Ⅱ)(理)由已知中函数f(x)=ax2+4x-2的解析式,结合(I)的结论,我们可得对称轴 ,我们分
,我们分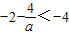 和
和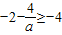 ,两种情况进行分类讨论,最后综合讨论结果,即可得到答案.
,两种情况进行分类讨论,最后综合讨论结果,即可得到答案.
(III)(理)由(2)知,当0<a<2,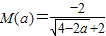 . 当a≥2,
. 当a≥2, . 我们根据分段函数分段处理的原则,分别求出各段上函数的最小值,即可得到,M(a)的最小值-3.
. 我们根据分段函数分段处理的原则,分别求出各段上函数的最小值,即可得到,M(a)的最小值-3.
(II)(文)由已知中当x∈[b,1]时,f(x)≥-2都成立,结合f(0)=-2,易得b≥0,进而得到b的最小值;
(Ⅲ)(文)由(Ⅱ)中的结论可知b≥0,进而可以判断出函数f(x)在区间[b,1]上为增函数,进而根据x∈[b,1]时,-2≤f(x)≤3b都成立,构造关于b的不等式,解不等式,即可得到实数b的取值范围.
解答:解:(Ⅰ)∵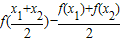
=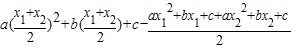
=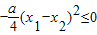 ,
,
∵x1≠x2,
∴a≥0.
∴实数a的取值范围为[0,+∞).
(Ⅱ)(理)∵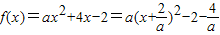 ,
,
显然f(0)=-2,对称轴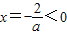 .
.
(1)当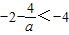 ,即0<a<2时,
,即0<a<2时,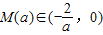 ,且f[M(a)]=-4.
,且f[M(a)]=-4.
令ax2+4x-2=-4,解得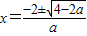 ,
,
此时M(a)取较大的根,即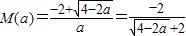 ,
,
(2)当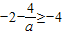 ,即a≥2时,
,即a≥2时, ,且f[M(a)]=4.
,且f[M(a)]=4.
令ax2+4x-2=4,解得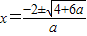 ,
,
此时M(a)取较小的根,即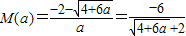 ,
,
(Ⅲ)(理) 由(2)知,
当0<a<2, . 此时 M(a)>-1
. 此时 M(a)>-1
当a≥2, . 此时 M(a)≥-3(当且仅当a=2时,取等号)
. 此时 M(a)≥-3(当且仅当a=2时,取等号)
∵-3<-1,
∴当a=2时,M(a)取得最小值-3.
(Ⅱ)(文)∵f(0)=-2
由x∈[b,1]时,f(x)≥-2都成立
∴b≥0
∴b的最小值为0
(Ⅲ)(文)由(Ⅱ)知 b≥0
∴f(x)在[b,1]上为增函数,
∴f(1)≤3b
即:a+4-2≤3b
又 由(Ⅰ)a≥0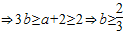
∴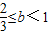
点评:本题考查的知识点是二次函数的图象和性质,一元二次方程的根的分布与系数的关系,分段函数的最小值,函数恒成立问题,其中(I)的关键是根据实数的性质,判断出实数a的取值范围,理科(II)的关键是根据函数f(x)=ax2+4x-2的对称轴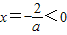 ,确定分类标准,(III)的关键是根据分段函数分段处理的原则,得到分段函数的最值,而文科(II)(III)的关键是根据已知条件构造关于b的不等式.
,确定分类标准,(III)的关键是根据分段函数分段处理的原则,得到分段函数的最值,而文科(II)(III)的关键是根据已知条件构造关于b的不等式.
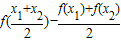 的解析式,并根据
的解析式,并根据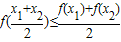 判断其符号,即可得到实数a的取值范围;
判断其符号,即可得到实数a的取值范围;(Ⅱ)(理)由已知中函数f(x)=ax2+4x-2的解析式,结合(I)的结论,我们可得对称轴
 ,我们分
,我们分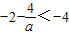 和
和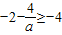 ,两种情况进行分类讨论,最后综合讨论结果,即可得到答案.
,两种情况进行分类讨论,最后综合讨论结果,即可得到答案.(III)(理)由(2)知,当0<a<2,
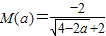 . 当a≥2,
. 当a≥2, . 我们根据分段函数分段处理的原则,分别求出各段上函数的最小值,即可得到,M(a)的最小值-3.
. 我们根据分段函数分段处理的原则,分别求出各段上函数的最小值,即可得到,M(a)的最小值-3.(II)(文)由已知中当x∈[b,1]时,f(x)≥-2都成立,结合f(0)=-2,易得b≥0,进而得到b的最小值;
(Ⅲ)(文)由(Ⅱ)中的结论可知b≥0,进而可以判断出函数f(x)在区间[b,1]上为增函数,进而根据x∈[b,1]时,-2≤f(x)≤3b都成立,构造关于b的不等式,解不等式,即可得到实数b的取值范围.
解答:解:(Ⅰ)∵
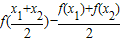
=
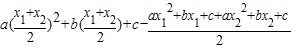
=
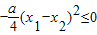 ,
,∵x1≠x2,
∴a≥0.
∴实数a的取值范围为[0,+∞).
(Ⅱ)(理)∵
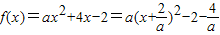 ,
,显然f(0)=-2,对称轴
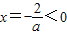 .
.(1)当
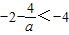 ,即0<a<2时,
,即0<a<2时,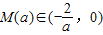 ,且f[M(a)]=-4.
,且f[M(a)]=-4.令ax2+4x-2=-4,解得
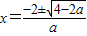 ,
,此时M(a)取较大的根,即
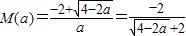 ,
,(2)当
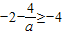 ,即a≥2时,
,即a≥2时, ,且f[M(a)]=4.
,且f[M(a)]=4.令ax2+4x-2=4,解得
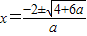 ,
,此时M(a)取较小的根,即
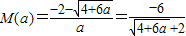 ,
,(Ⅲ)(理) 由(2)知,
当0<a<2,
 . 此时 M(a)>-1
. 此时 M(a)>-1当a≥2,
 . 此时 M(a)≥-3(当且仅当a=2时,取等号)
. 此时 M(a)≥-3(当且仅当a=2时,取等号)∵-3<-1,
∴当a=2时,M(a)取得最小值-3.
(Ⅱ)(文)∵f(0)=-2
由x∈[b,1]时,f(x)≥-2都成立
∴b≥0
∴b的最小值为0
(Ⅲ)(文)由(Ⅱ)知 b≥0
∴f(x)在[b,1]上为增函数,
∴f(1)≤3b
即:a+4-2≤3b
又 由(Ⅰ)a≥0
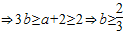
∴
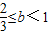
点评:本题考查的知识点是二次函数的图象和性质,一元二次方程的根的分布与系数的关系,分段函数的最小值,函数恒成立问题,其中(I)的关键是根据实数的性质,判断出实数a的取值范围,理科(II)的关键是根据函数f(x)=ax2+4x-2的对称轴
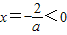 ,确定分类标准,(III)的关键是根据分段函数分段处理的原则,得到分段函数的最值,而文科(II)(III)的关键是根据已知条件构造关于b的不等式.
,确定分类标准,(III)的关键是根据分段函数分段处理的原则,得到分段函数的最值,而文科(II)(III)的关键是根据已知条件构造关于b的不等式. 
练习册系列答案
相关题目