题目内容
已知向量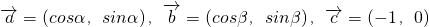
(1)求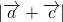 的最大值
的最大值
(2)若 ,且
,且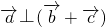 ,求cosβ的值.
,求cosβ的值.
解:(1) =(cosβ-1,sinβ),则
=(cosβ-1,sinβ),则
| |2=(cosβ-1)2+sin2β=2(1-cosβ).
|2=(cosβ-1)2+sin2β=2(1-cosβ).
∵-1≤cosβ≤1,
∴0≤| |2≤4,即0≤|
|2≤4,即0≤| |≤2.
|≤2.
当cosβ=-1时,有| |=2,
|=2,
所以向量 的长度的最大值为2.
的长度的最大值为2.
(2)由(1)可得 =(cosβ-1,sinβ),
=(cosβ-1,sinβ),
 •(
•( )=cosαcosβ+sinαsinβ-cosα=cos(α-β)-cosα.
)=cosαcosβ+sinαsinβ-cosα=cos(α-β)-cosα.
∵ ⊥(
⊥( ),
),
∴ •(
•( )=0,即cos(α-β)=cosα.
)=0,即cos(α-β)=cosα.
由 ,
,
得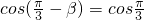 ,
,
即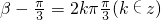 .
.
∴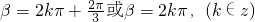 ,
,
于是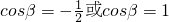 .…(14分).
.…(14分).
分析:(1)利用向量的运算法则求出 ,利用向量模的平方等于向量的平方求出
,利用向量模的平方等于向量的平方求出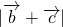 的平方,利用三角函数的平方关系将其化简,利用三角函数的有界性求出最值.
的平方,利用三角函数的平方关系将其化简,利用三角函数的有界性求出最值.
(2)利用向量垂直的充要条件列出方程,利用两角差的余弦公式化简得到的等式,求出值.
点评:本题考查向量模的性质:向量模的平方等于向量的平方、向量垂直的充要条件;三角函数的平方关系、三角函数的有界性、两角差的余弦公式.考查计算能力.
 =(cosβ-1,sinβ),则
=(cosβ-1,sinβ),则|
 |2=(cosβ-1)2+sin2β=2(1-cosβ).
|2=(cosβ-1)2+sin2β=2(1-cosβ).∵-1≤cosβ≤1,
∴0≤|
 |2≤4,即0≤|
|2≤4,即0≤| |≤2.
|≤2.当cosβ=-1时,有|
 |=2,
|=2,所以向量
 的长度的最大值为2.
的长度的最大值为2.(2)由(1)可得
 =(cosβ-1,sinβ),
=(cosβ-1,sinβ), •(
•( )=cosαcosβ+sinαsinβ-cosα=cos(α-β)-cosα.
)=cosαcosβ+sinαsinβ-cosα=cos(α-β)-cosα.∵
 ⊥(
⊥( ),
),∴
 •(
•( )=0,即cos(α-β)=cosα.
)=0,即cos(α-β)=cosα.由
 ,
,得
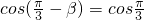 ,
,即
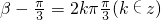 .
.∴
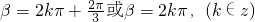 ,
,于是
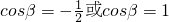 .…(14分).
.…(14分).分析:(1)利用向量的运算法则求出
 ,利用向量模的平方等于向量的平方求出
,利用向量模的平方等于向量的平方求出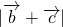 的平方,利用三角函数的平方关系将其化简,利用三角函数的有界性求出最值.
的平方,利用三角函数的平方关系将其化简,利用三角函数的有界性求出最值.(2)利用向量垂直的充要条件列出方程,利用两角差的余弦公式化简得到的等式,求出值.
点评:本题考查向量模的性质:向量模的平方等于向量的平方、向量垂直的充要条件;三角函数的平方关系、三角函数的有界性、两角差的余弦公式.考查计算能力.

练习册系列答案
相关题目
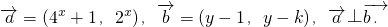
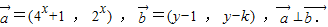

 的最大值;
的最大值; ,求点P(x,y)的轨迹方程及
,求点P(x,y)的轨迹方程及 的最大值.
的最大值.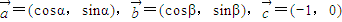
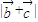 的最大值
的最大值 ,且
,且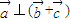 ,求cosβ的值.
,求cosβ的值.