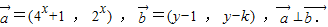题目内容
已知向量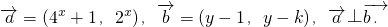
(1)求函数y=f(x)的解析式;
(2)若函数f(x)的最小值为-3,求实数k的值;
(3)若对任意实数x1,x2,x3,均存在以f(x1),f(x2),f(x3)为三边长的三角形,求实数k的取值范围.
解:(1)∵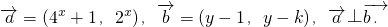
∴(4x+1)(y-1)+2x(y-k)=0,化简整理得y(4x+2x+1)=4x+k•2x+1
因此,函数y=f(x)的解析式为y=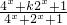 ;
;
(2)∵f(x)=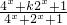 =1+
=1+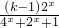
∴根据函数f(x)的最小值为-3,得t=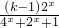 的最小值为-4
的最小值为-4
∵2x+2-x+1≥2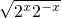 +1=3
+1=3
∴当k>1时,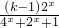 =
=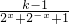 ≤
≤ ;当k<1时,
;当k<1时,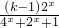 =
=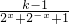 ≥
≥ ;
;
k=1时,函数f(x)=1恒成立不符合题意.
∴结合题意可得k<1,且当且仅当2x=2-x=1,即x=0时,t的最小值为 =-4,解之得k=-11
=-4,解之得k=-11
即函数f(x)的最小值为-3时,实数k的值为-11;
(3)∵对任意实数x1、x2、x3,都存在以f(x1)、f(x2)、f(x3)为三边长的三角形,
∴f(x1)+f(x2)>f(x3)对任意的x1、x2、x3∈R恒成立.
当k>1时,因为2<f(x1)+f(x2)≤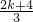 且1<f(x3)≤
且1<f(x3)≤ ,
,
∴ ≤2,解之得1<k≤4;
≤2,解之得1<k≤4;
当k=1时,可得f(x1)=f(x2)=f(x3)=1,满足题意的条件;
当k<1时,因为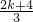 ≤f(x1)+f(x2)<2,且
≤f(x1)+f(x2)<2,且 ≤f(x3)<1,
≤f(x3)<1,
∴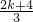 ≥1,解之得-
≥1,解之得- ≤k<1;
≤k<1;
综上所述,实数k的取值范围是[- ,4]
,4]
分析:(1)根据向量垂直的充要条件的坐标表示式,建立关于x、y的等式,从中解出用x表示y的式子,即可得到函数y=f(x)的解析式.
(2)将f(x)表达式的分子、分母都除以2x,得到它的分母2x+2-x+1≥2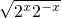 +1=3.再根据k与1的大小关系分类讨论,即可得到必定有k<1,且当2x=2-x=1即x=0时,函数有最小值为-3,由此解关于k的等式即得实数k的值.
+1=3.再根据k与1的大小关系分类讨论,即可得到必定有k<1,且当2x=2-x=1即x=0时,函数有最小值为-3,由此解关于k的等式即得实数k的值.
(3)根据构成三角形的条件,得出不等式f(x1)+f(x2)>f(x3)恒成立,然后分三种情况进行讨论,转化为f(x1)+f(x2)的最小值与f(x3)的最大值的不等式,进而可以求出实数k 的取值范围.
点评:本题以向量的数量积运算为载体,求函数的表达式并讨论函数的最值.着重考查了向量数量积公式、基本不等式求最值、函数恒成立等知识,属于中档题.
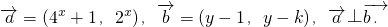
∴(4x+1)(y-1)+2x(y-k)=0,化简整理得y(4x+2x+1)=4x+k•2x+1
因此,函数y=f(x)的解析式为y=
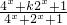 ;
;(2)∵f(x)=
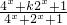 =1+
=1+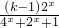
∴根据函数f(x)的最小值为-3,得t=
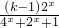 的最小值为-4
的最小值为-4∵2x+2-x+1≥2
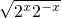 +1=3
+1=3∴当k>1时,
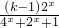 =
=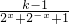 ≤
≤ ;当k<1时,
;当k<1时,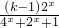 =
=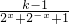 ≥
≥ ;
;k=1时,函数f(x)=1恒成立不符合题意.
∴结合题意可得k<1,且当且仅当2x=2-x=1,即x=0时,t的最小值为
 =-4,解之得k=-11
=-4,解之得k=-11即函数f(x)的最小值为-3时,实数k的值为-11;
(3)∵对任意实数x1、x2、x3,都存在以f(x1)、f(x2)、f(x3)为三边长的三角形,
∴f(x1)+f(x2)>f(x3)对任意的x1、x2、x3∈R恒成立.
当k>1时,因为2<f(x1)+f(x2)≤
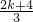 且1<f(x3)≤
且1<f(x3)≤ ,
,∴
 ≤2,解之得1<k≤4;
≤2,解之得1<k≤4;当k=1时,可得f(x1)=f(x2)=f(x3)=1,满足题意的条件;
当k<1时,因为
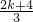 ≤f(x1)+f(x2)<2,且
≤f(x1)+f(x2)<2,且 ≤f(x3)<1,
≤f(x3)<1,∴
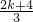 ≥1,解之得-
≥1,解之得- ≤k<1;
≤k<1;综上所述,实数k的取值范围是[-
 ,4]
,4]分析:(1)根据向量垂直的充要条件的坐标表示式,建立关于x、y的等式,从中解出用x表示y的式子,即可得到函数y=f(x)的解析式.
(2)将f(x)表达式的分子、分母都除以2x,得到它的分母2x+2-x+1≥2
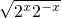 +1=3.再根据k与1的大小关系分类讨论,即可得到必定有k<1,且当2x=2-x=1即x=0时,函数有最小值为-3,由此解关于k的等式即得实数k的值.
+1=3.再根据k与1的大小关系分类讨论,即可得到必定有k<1,且当2x=2-x=1即x=0时,函数有最小值为-3,由此解关于k的等式即得实数k的值.(3)根据构成三角形的条件,得出不等式f(x1)+f(x2)>f(x3)恒成立,然后分三种情况进行讨论,转化为f(x1)+f(x2)的最小值与f(x3)的最大值的不等式,进而可以求出实数k 的取值范围.
点评:本题以向量的数量积运算为载体,求函数的表达式并讨论函数的最值.着重考查了向量数量积公式、基本不等式求最值、函数恒成立等知识,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目