题目内容
已知向量
(1)求
 的最大值;
的最大值;(2)若m>0,向量
 ,求点P(x,y)的轨迹方程及
,求点P(x,y)的轨迹方程及 的最大值.
的最大值.
【答案】分析:(1)因为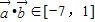 ,则msinx+n∈[-7,1],当m>0时,
,则msinx+n∈[-7,1],当m>0时,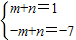 ;当m<0时,
;当m<0时,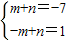 ,由此能求出最大值.
,由此能求出最大值.
(2)由于 m>0,则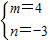 ,所以
,所以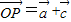 =(4+cosx,-3+sinx)=(x,y),由此能求出点P(x,y)的轨迹方程及
=(4+cosx,-3+sinx)=(x,y),由此能求出点P(x,y)的轨迹方程及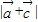 的最大值.
的最大值.
解答:解:(1)因为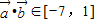 ,
,
则msinx+n∈[-7,1],
当m>0时,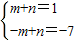 ,
,
解得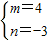 ;
;
当m<0时, ,
,
解得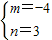 .
.
所以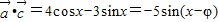 ,
,
由于x∈R,∴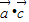 的最大值为5
的最大值为5
(2)由于 m>0,
则由(1)知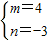 ,
,
∵向量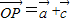 ,点P(x,y)
,点P(x,y)
∴ =(4+cosx,-3+sinx)=(x,y)
=(4+cosx,-3+sinx)=(x,y)
∴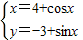 ,
,
故点P(x,y)的轨迹方程为:(x-4)2+(y+3)2=1;
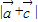 =|(4+cosx,-3+sinx)|
=|(4+cosx,-3+sinx)|
=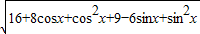
=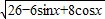
=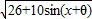 ,
,
∴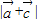 的最大值为6.
的最大值为6.
点评:本题考查求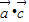 的最大值;若m>0,向量
的最大值;若m>0,向量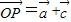 ,求点P(x,y)的轨迹方程及
,求点P(x,y)的轨迹方程及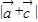 的最大值.解题时要认真审题,仔细解答,注意合理地进行等价转化.
的最大值.解题时要认真审题,仔细解答,注意合理地进行等价转化.
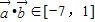 ,则msinx+n∈[-7,1],当m>0时,
,则msinx+n∈[-7,1],当m>0时,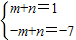 ;当m<0时,
;当m<0时,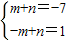 ,由此能求出最大值.
,由此能求出最大值.(2)由于 m>0,则
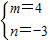 ,所以
,所以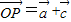 =(4+cosx,-3+sinx)=(x,y),由此能求出点P(x,y)的轨迹方程及
=(4+cosx,-3+sinx)=(x,y),由此能求出点P(x,y)的轨迹方程及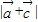 的最大值.
的最大值.解答:解:(1)因为
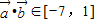 ,
,则msinx+n∈[-7,1],
当m>0时,
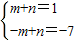 ,
,解得
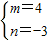 ;
;当m<0时,
 ,
,解得
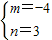 .
.所以
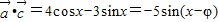 ,
,由于x∈R,∴
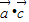 的最大值为5
的最大值为5(2)由于 m>0,
则由(1)知
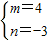 ,
,∵向量
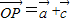 ,点P(x,y)
,点P(x,y)∴
 =(4+cosx,-3+sinx)=(x,y)
=(4+cosx,-3+sinx)=(x,y)∴
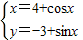 ,
,故点P(x,y)的轨迹方程为:(x-4)2+(y+3)2=1;
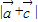 =|(4+cosx,-3+sinx)|
=|(4+cosx,-3+sinx)|=
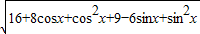
=
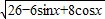
=
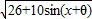 ,
,∴
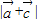 的最大值为6.
的最大值为6.点评:本题考查求
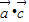 的最大值;若m>0,向量
的最大值;若m>0,向量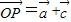 ,求点P(x,y)的轨迹方程及
,求点P(x,y)的轨迹方程及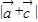 的最大值.解题时要认真审题,仔细解答,注意合理地进行等价转化.
的最大值.解题时要认真审题,仔细解答,注意合理地进行等价转化. 
练习册系列答案
相关题目
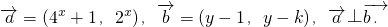
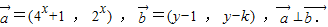
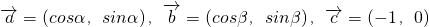
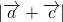 的最大值
的最大值 ,且
,且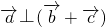 ,求cosβ的值.
,求cosβ的值.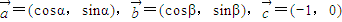
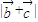 的最大值
的最大值 ,且
,且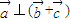 ,求cosβ的值.
,求cosβ的值.