题目内容
在线段[0,1]上任意投三个点,问由0至1三个点的三条线段,能构成三角形与不能构成三角形的两个事件中,哪一个事件的概率大?
分析:设三条线段的长分别为x、y、1-x-y,分别建立所有的基本事件满足不等式组和三条线段能构成三角形事件满足的不等式组,在平面直角坐标系作出不等式组对应的平面区域,得到如图的△OAB与△CDE,计算出△CDE与△OAB的面积比,可得三条线段能构成三角形的概率P(A)=
,进而得到三条线段不能构成三角形的概率,由此即可得到本题的答案.
| 1 |
| 4 |
解答:解: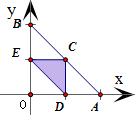 设三条线段的长分别为x、y、1-x-y
设三条线段的长分别为x、y、1-x-y
则所有的基本事件满足不等式组
,
对应如图坐标系中的三角形OAB及其内部;
事件A=“三条线段能构成三角形”,
事件A满足不等式组
,化简得
对应如图坐标系中的三角形CDE及其内部
∵C、D、E分别为三角形OAB各边的中点,
∴三角形CDE与三角形OAB的面积比为
=
因此,三条线段能构成三角形的概率P(A)=
=
从而三条线段不能构成三角形的概率P(
)=1-P(A)=
答:能构成三角形与不能构成三角形的两个事件中,不能构成三角形事件的概率大.
 设三条线段的长分别为x、y、1-x-y
设三条线段的长分别为x、y、1-x-y则所有的基本事件满足不等式组
|
对应如图坐标系中的三角形OAB及其内部;
事件A=“三条线段能构成三角形”,
事件A满足不等式组
|
|
对应如图坐标系中的三角形CDE及其内部
∵C、D、E分别为三角形OAB各边的中点,
∴三角形CDE与三角形OAB的面积比为
| S△CDE |
| S△OAB |
| 1 |
| 4 |
因此,三条线段能构成三角形的概率P(A)=
| S△CDE |
| S△OAB |
| 1 |
| 4 |
从而三条线段不能构成三角形的概率P(
. |
| A |
| 3 |
| 4 |
答:能构成三角形与不能构成三角形的两个事件中,不能构成三角形事件的概率大.
点评:本题给出线段[0,1]上两个点将线段分成三条线段,求三条线段能构成三角形的概率.着重考查了二元一次不等式表示的平面区域和几何概型及其应用等知识,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
在线段[0,3]上任取一点,则此点坐标大于1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|















