题目内容
12.求下列函数的值域:y=2x-$\sqrt{1-x}$.分析 可由1-x≥0得出x的范围,从而得出2x≤2,并且$-\sqrt{1-x}≤0$,从而可以得出y的范围,即得出该函数的值域.
解答 解:1-x≥0;
∴$-\sqrt{1-x}≤0$,x≤1,2x≤2;
∴$2x-\sqrt{1-x}≤2$;
即y≤2;
∴该函数的值域为(-∞,2].
点评 考查函数值域的概念,根据不等式的性质求函数值域的方法.

练习册系列答案
相关题目
15.已知角α的终边经过点P(0,1),则tanα=( )
| A. | 0 | B. | -4 | C. | 4 | D. | 不存在 |
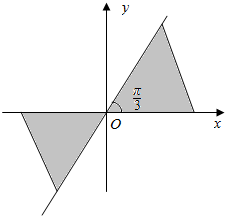 如图所示,阴影部分表示的角的集合为(含边界){α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}(用弧度表示).
如图所示,阴影部分表示的角的集合为(含边界){α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}(用弧度表示).