题目内容

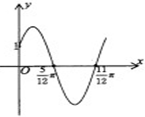若函数f（x）=Asin（ωx+φ）的部分图象如图所示，其中A＞0，ω＞0，0＜φ＜
π
2
，则f（x）=（　　）
分析：由
1
2
T=
π
2
可求得ω，再由
5π
12
ω+φ=π可求φ，最后由f（0）=1可求A．
解答：解：∵
1
2
T=
11π
12
-
5π
12
=
π
2
，ω＞0，
∴T=
2π
ω
=π，
∴ω=2；
又
5π
12
×2+φ=π，
∴φ=
π
6
；
∴f（x）=Asin（2x+
π
6
），
又f（0）=Asin
π
6
=1，
∴A=2．
∴f（x）=2sin（2x+
π
6
）．
故选B．
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求得φ是难点，属于中档题．
练习册系列答案
相关题目
设函数f（x）的定义域为R，当x＜0时f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）．数列{an}满足f（an+1）=
1f(-2-an)
（n∈N*）
（Ⅰ）求f（0）的值，判断并证明函数f（x）的单调性；
（Ⅱ）如果存在t、s∈N*，s≠t，使得点（t，as）、（s，at）都在直线y=kx-1上，试判断是否存在自然数M，当n＞M时，a n＞f（0）恒成立？若存在，求出M的最小值，若不存在，请说明理由．
设函数f（x）的定义域为R，当x＜0时f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）．数列{an}满足f(an+1)=
1
f(-2-an)
(n∈N*)．
（Ⅰ）求f（0）的值，判断并证明函数f（x）的单调性；
（Ⅱ）如果存在t、s∈N*，s≠t，使得点（t，as）、（s，at）都在直线y=kx-1上，试判断是否存在自然数M，当n＞M时，an＞0恒成立？若存在，求出M的最小值，若不存在，请说明理由；
（Ⅲ）若a1=f（0），不等式
1
an+1
+
1
an+2
+…+
1
a2n
＞
12
35
(1+logf(1)x)对不小于2的正整数恒成立，求x的取值范围．
设函数f（x）=
3x-1
x+1
．
（1）已知s=-t+
1
2
（t＞1），求证：f（
t-1
t
）=
s+1
s
；
（2）证明：存在函数t=φ（s）=as+b（s＞0），满足f（
s+1
s
）=
t-1
t
；
（3）设x1=
11
17
，xn+1=f（xn），n=1，2，…．问：数列{
1
xn-1
}是否为等差数列？若是，求出数列{xn}中最大项的值；若不是，请说明理由．
设函数f（x）的定义域为R，当x＜0时f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）．数列{an}满足f（an+1）=（n∈N*）
（Ⅰ）求f（0）的值，判断并证明函数f（x）的单调性；
（Ⅱ）如果存在t、s∈N*，s≠t，使得点（t，as）、（s，at）都在直线y=kx-1上，试判断是否存在自然数M，当n＞M时，a n＞f（0）恒成立？若存在，求出M的最小值，若不存在，请说明理由．
设函数f（x）的定义域为R，当x＜0时f（x）＞1，且对任意的实数x，y∈R，有f（x+y）=f（x）f（y）．数列{an}满足．
（Ⅰ）求f（0）的值，判断并证明函数f（x）的单调性；
（Ⅱ）如果存在t、s∈N*，s≠t，使得点（t，as）、（s，at）都在直线y=kx-1上，试判断是否存在自然数M，当n＞M时，an＞0恒成立？若存在，求出M的最小值，若不存在，请说明理由；
（Ⅲ）若a1=f（0），不等式对不小于2的正整数恒成立，求x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网