题目内容
二次函数y=f（x）满足：①f（0）=1；②f（x+1）-f（x）=2x．（1）求f（x）的解析式；
（2）求f（x）在区间[-1，1]上的最大值和最小值；
分析：（1）先由f（0）=1，求得c，再由②f（x+1）-f（x）=2x．用待定系数法求得其解析式．
（2）先配方，求出其对称轴，再根据对称轴与区间的关系，求得最值．
（2）先配方，求出其对称轴，再根据对称轴与区间的关系，求得最值．
解答：解：（1）设y=ax2+bx+c（a≠0）（1分）
由f（0）=1得，c=1（2分）
因为f（x+1）-f（x）=2x所以a（x+1）2+b（x+1）-ax2-bx=2x，
即2ax+a+b=2x（7分）
所以
?
（9分）
所以f（x）=x2-x+1（10分）
（2）f(x)=(x-
)2+
，x∈[-1，1]（12分）
当x=
时，ymin=
，（14分）
当x=-1时，ymax=3．（16分）
由f（0）=1得，c=1（2分）
因为f（x+1）-f（x）=2x所以a（x+1）2+b（x+1）-ax2-bx=2x，
即2ax+a+b=2x（7分）
所以
|
|
所以f（x）=x2-x+1（10分）
（2）f(x)=(x-
| 1 |
| 2 |
| 3 |
| 4 |
当x=
| 1 |
| 2 |
| 3 |
| 4 |
当x=-1时，ymax=3．（16分）
点评：本题主要考查用待定系数法求二次函数解析式和用配方法来研究二次函数的单调性及最值问题．
练习册系列答案
相关题目
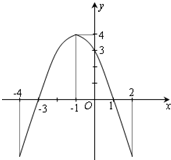如图是一个二次函数y=f（x）的图象．
已知二次函数y=f（x）的图象如图所示．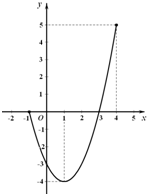
二次函数y=f（x）的图象的一部分如图所示．