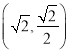题目内容
【题目】已知函数 
， 
，若f（x）≤g（x）在区间[0，1]上恒成立，则（ ）
A.实数t有最小值1
B.实数t有最大值1
C.实数t有最小值 
D.实数t有最大值
【答案】A
【解析】解：若对任意的x∈[0，1]，有f（x）≤g（x）恒成立，则对任意的x∈[0，1]，有g（x）﹣f（x）≥0恒成立，
令h（x）=g（x）﹣f（x）= 
，x∈[0，1]，
则h′（x）=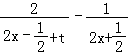 
= 
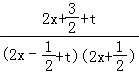，x＞max{ 
， 
}．
由题意可得 
，即t 
，再由h′（x）=0，可得x= 
≤﹣1，
则h（x）在[0，1]上单调递增， 
，解得t≥1．
∴实数t有最小值1．
故选：A．
【考点精析】通过灵活运用函数的最大(小)值与导数，掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值即可以解答此题．
练习册系列答案
相关题目
