题目内容
某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.
(I)设所选5人中女医生的人数为ξ,求ξ的分布列及数学期望;
(II)现从10名医生中的张强、李军、王刚、赵永4名男医生,李莉、孙萍2名女医生共6人中选一正二副3名组长,在张强被选中的情况下,求李莉也被选中的概率.
(I)设所选5人中女医生的人数为ξ,求ξ的分布列及数学期望;
(II)现从10名医生中的张强、李军、王刚、赵永4名男医生,李莉、孙萍2名女医生共6人中选一正二副3名组长,在张强被选中的情况下,求李莉也被选中的概率.
分析:(I)由题意知变量的可能的取值是0,1,2,3,集合变量对应的事件和等可能事件的概率公式,写出变量对应的概率,写出分布列和期望值.
(II)张强被选中的情况下李莉也被选中的概率,是一个条件概率,做出两个人同时被选中的概率,除以张强被选中的概率,得到结果.
(II)张强被选中的情况下李莉也被选中的概率,是一个条件概率,做出两个人同时被选中的概率,除以张强被选中的概率,得到结果.
解答:解:(I)ξ的所有可能的取值为0,1,2,3,….….(2分)
则P(ξ=0)=
=
P(ξ=1)=
=
P(ξ=2)=
=
;
P(ξ=3)=
=
…(6分)
ξ.的分布列为
Eξ=1×
+2×
+3×
=
…(9分)
(II)记“张强被选中”为事件A,“李莉也被选中”为事件B,
则P(A)=
=
,P(BA)=
=
,
所以P(B|A)=
=
…(12分)
则P(ξ=0)=
| ||
|
| 1 |
| 12 |
P(ξ=1)=
| ||||
|
| 5 |
| 12 |
P(ξ=2)=
| ||||
|
| 5 |
| 12 |
P(ξ=3)=
| ||||
|
| 1 |
| 12 |
ξ.的分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 12 |
| 5 |
| 12 |
| 1 |
| 12 |
| 3 |
| 2 |
(II)记“张强被选中”为事件A,“李莉也被选中”为事件B,
则P(A)=
| ||
|
| 1 |
| 2 |
| ||
|
| 1 |
| 5 |
所以P(B|A)=
| P(BA) |
| P(A) |
| 2 |
| 5 |
点评:本题考查离散型随机变量的分布列和期望,以及条件概率是问题,本题解题的关键是理解变量对应的事件,本题是一个中档题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
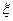 ,求
,求 12分)某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.
12分)某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.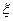 ,求
,求 的分布列及数学期望;
的分布列及数学期望;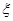 ,求
,求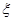 ,求
,求