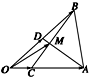
题目内容
如图所示，在△ABO中，
=
,
=
,AD与BC相交于点M，设=a，=b.试用a和b表示向量
.
=
a+
b
解析:
设
=ma+nb，
则
=-
=ma+nb-a=(m-1)a+nb.
=
-=
-=-a+b.
又∵A、M、D三点共线，∴与共线.
∴存在实数t,使得=t，
即(m-1)a+nb=t(-a+b). 4分
∴(m-1)a+nb=-ta+tb.
|
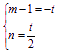，消去t得：m-1=-2n. 即m+2n=1. ① 6分
又∵
=-
=ma+nb-
a=(m-)a+nb.
=-=b-a=-a+b.
又∵C、M、B三点共线，∴与共线. 10分
∴存在实数t1,使得=t1,
|
)a+nb=t1
, ∴
，
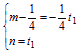消去t1得,4m+n=1 ② 12分
由①②得m=,n=,
∴=a+b. 14分
练习册系列答案
相关题目
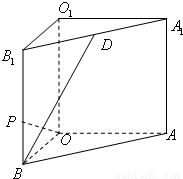
如图所示，A、B是在同一水平面上相距am的两处雷达站，A在B的正西方，突然两台雷达同时发现天空O位置处一不明飞行物正以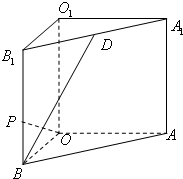
如图所示，在直三棱柱ABO-A1B1O1中，OO1=4，OA=4，OB=3，∠AOB=90°，D是线段A1B1的中点，P是侧棱BB1上的一点．若OP⊥BD，求三棱锥D-OPB的体积．
=
,
=
,AD与BC相交于点M，设
.
