Question

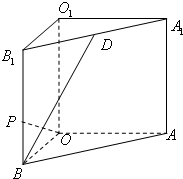如图所示，在直三棱柱ABO-A₁B₁O₁中，OO₁=4，OA=4，OB=3，∠AOB=90°，D是线段A₁B₁的中点，P是侧棱BB₁上的一点．若OP⊥BD，求三棱锥D-OPB的体积．

Answer 1

分析：以OB所在的直线为x轴，以OA所在的直线为y轴，以OO₁所在的直线为z轴，建立空间直角坐标系，根据OP⊥BD，可求出点P的坐标，从而求出底面积S_△OPB的面积，根据锥体的体积公式求解即可求出所求．

解答：解：以OB所在的直线为x轴，以OA所在的直线为y轴，以OO₁所在的直线为z轴，建立如图所示的空间直角坐标系，则B（3，0，0）、A（0，4，0）、A₁（0，4，4），
设P（3，0，m）∵

OP

⊥

BD

∴

OP

•

BD

=-

9

2

+4m=0∴m=

9

8

------------------------（6分）
即BP=

9

8

-----------------------（8分）
VD-OPB=

1

3

S△OPB•2=

2

3

•

1

2

×3×

9

8

=

9

8

-------------------------（12分）

点评：本题主要考查了利用空间向量的方法求解立体几何问题，同时考查了锥体的体积的计算，属于中档题．