题目内容
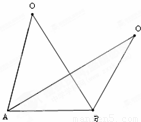
 如图所示,A、B是在同一水平面上相距am的两处雷达站,A在B的正西方,突然两台雷达同时发现天空O位置处一不明飞行物正以100
如图所示,A、B是在同一水平面上相距am的两处雷达站,A在B的正西方,突然两台雷达同时发现天空O位置处一不明飞行物正以100| 6 |
分析:设AO’与BO交于点M,由题意可求∠ABO,∠BAO′,OO′,从而可求∠AMB=90°,利用锐角三角函数可求AM,然后结合∠MAO=∠AOM=45°,在Rt△AMB中,可得AM=OM,进而可得MO′=AM=
=OM,可得OO′=
MO′=
a,代入即可求解
| ||
| 2 |
| 2 |
| ||
| 2 |
解答:解:设AO’与BO交于点M
由题意可得,∠ABO=60°,∠O‘AB=30°,OO′=100
×
×60=9000
∴∠AMB=90°,AM=
且∠MAO=∠AOM=45°
Rt△AMB中,AM=OM=
a
∵∠ABO′=120°,∠BAO′=30°,
∴∠BO′A=30°
∴MO′=AM=
=OM
∴OO′=
MO′=
a=150
×60
∴a=18000米
由题意可得,∠ABO=60°,∠O‘AB=30°,OO′=100
| 6 |
| 3 |
| 2 |
| 6 |
∴∠AMB=90°,AM=
| ||
| 2 |
且∠MAO=∠AOM=45°
Rt△AMB中,AM=OM=
| ||
| 2 |
∵∠ABO′=120°,∠BAO′=30°,
∴∠BO′A=30°
∴MO′=AM=
| ||
| 2 |
∴OO′=
| 2 |
| ||
| 2 |
| 6 |
∴a=18000米
点评:本题考查的是解直角三角形的应用-方向角问题,熟练掌握基本知识并能灵活应用是解答此题的关键.

练习册系列答案
相关题目

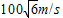 沿直线OO′飞行,并在O位置时测得∠BAO=75°,∠ABO=60°.雷达继续跟踪此飞行物,经过1.5min 后,飞行物到达O′,并 测得∠BAO′=30°,∠ABO′=120°,求两雷达观察站A和B之间距离a的大小.
沿直线OO′飞行,并在O位置时测得∠BAO=75°,∠ABO=60°.雷达继续跟踪此飞行物,经过1.5min 后,飞行物到达O′,并 测得∠BAO′=30°,∠ABO′=120°,求两雷达观察站A和B之间距离a的大小.