题目内容
已知抛物线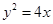 的焦点
的焦点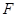 与椭圆
与椭圆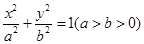 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为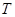 ,且
,且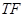 与
与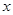 轴垂直,则椭圆的离心率为( )
轴垂直,则椭圆的离心率为( )
A.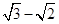 | B.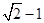 | C.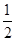  | D. |
B.
解析试题分析:因为抛物线 的焦点
的焦点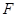 与椭圆
与椭圆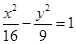 的一个焦点重合.所以椭圆的c=1,又因为
的一个焦点重合.所以椭圆的c=1,又因为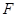 与
与 轴垂直,所以交点T的坐标为(1,2)代入椭圆方程即可得
轴垂直,所以交点T的坐标为(1,2)代入椭圆方程即可得 ,又因为c=1,所以
,又因为c=1,所以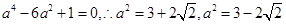 (舍去).所以
(舍去).所以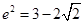 .通过计算四个选项可得应该选B.本题由抛物线的焦点坐标,再列出一个关于
.通过计算四个选项可得应该选B.本题由抛物线的焦点坐标,再列出一个关于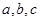 的一个方程.即可求出e,但计算稍微复杂些,含根号式子的开方不熟练,可以通过把答案平方来求的结果.
的一个方程.即可求出e,但计算稍微复杂些,含根号式子的开方不熟练,可以通过把答案平方来求的结果.
考点:1.抛物线的知识.2.椭圆中三个基本量的方程.3.离心率的概念.4.双二次方程的解法.

练习册系列答案
相关题目
抛物线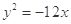 的准线与双曲线
的准线与双曲线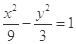 的两条渐近线所围成的三角形的面积等于( )
的两条渐近线所围成的三角形的面积等于( )
A.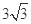 | B. | C.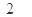 | D.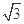 |
已知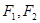 是椭圆
是椭圆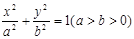 的两个焦点,
的两个焦点, 是过
是过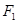 的弦,则
的弦,则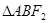 的周长是( )
的周长是( )
A.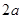 | B. | C.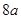 | D.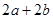 |
设椭圆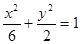 和双曲线
和双曲线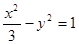 的公共焦点为
的公共焦点为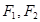 ,
,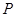 是两曲线的一个公共点,则cos
是两曲线的一个公共点,则cos 的值等于( )
的值等于( )
A.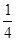 | B.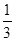 | C. | D.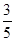 |
抛物线y2=4px(p>0)上一点M到焦点的距离为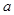 ,则M到y轴距离为 ( )
,则M到y轴距离为 ( )
| A.a-p | B.a+p | C.a-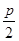 | D.a+2p |
在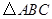 中,
中,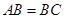 ,
,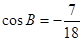 .若以
.若以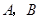 为焦点的椭圆经过点
为焦点的椭圆经过点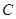 ,则该椭圆的离心率
,则该椭圆的离心率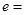 ( )
( )
A.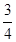 | B.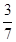 | C.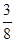 | D.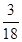 |
若抛物线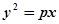 的焦点与椭圆
的焦点与椭圆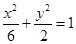 的右焦点重合,则
的右焦点重合,则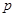 的值为( )
的值为( )
| A.8 | B.2 | C.-4 | D.4 |
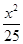 +
+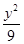 =1,F1、F2分别为其左、右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长为( )
=1,F1、F2分别为其左、右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长为( )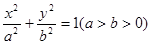 ,以O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A、B,若四边形PAOB为正方形,则椭圆的离心率为( )
,以O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A、B,若四边形PAOB为正方形,则椭圆的离心率为( )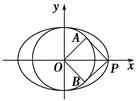
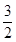 B.
B.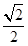 C.
C.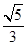 D.
D.