Question

已知递增的等比数列{}满足：，且是的等差中项．

（1）求数列{}的通项公式；

（2）若，，对任意正整数n，＜0恒成立，试求m的取值范围。

Answer 1

解、（1）设等比数列{a_n}的首项为a₁，公比为q．依题意，

有2（a₃＋2）＝a₂＋a₄，代入a₂＋a₃＋a₄＝28，得a₃＝8．

∴a₂＋a₄＝20．∴解之得，或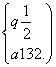

又{a_n}单调递增，∴q＝2，a₁＝2，∴a_n＝2ⁿ，  ………6分  

（2）b_n＝2ⁿ·log2ⁿ＝－n·2ⁿ，

∴－S_n＝1×2＋2×2²＋3×2³＋…＋n×2ⁿ①

－2S_n＝1×2²＋2×2³＋…＋（n－1）2ⁿ＋n·2^n＋1②

①－②得，S_n＝2＋2²＋2³＋…＋2ⁿ－n·2^n＋1

＝－n·2^n＋1

＝2^n＋1－2－n·2^n＋1

由S_n＋（n＋m）a_n＋1＜0，

即2^n＋1－2－n·2^n＋1＋n·2^n＋1＋m·2^n＋1＜0对任意正整数n恒成立，

∴m·2^n＋1＜2－2^n＋1．对任意正整数n，m＜－1恒成立．

∵－1＞－1，∴m≤－1．即m的取值范围是（－∞，－1]．………12分