题目内容
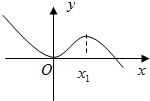 如图,函数f(x)=ax3+bx2+cx+d图象与x轴相切于原点.
如图,函数f(x)=ax3+bx2+cx+d图象与x轴相切于原点.(1)求证:b>0
(2)已知x1=1,设g(x)=ex2,若在[0,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数b的取值范围.
分析:(1)根据图象可得到函数在x=0处的函数值与导数都等于0,就可求出c,d的值,再通过图象判断函数的单调性,得到导数取正值和负值的范围,因为导数是关于x的二次函数,根据导数何时取正值,何时取负值,就可判断a的符号,和对称轴的符号,进而得到b的范围.
(2)先由x1=1,得f′(1)=0,从而f(x)=-
bx3+bx2,再构造新函数h(x))=f(x)-g(x)=-
bx3+(b-e)x2=x2(-
bx+b-e),若在[0,e]上至少存在一点x0,使得f(x0)>g(x0)成立,只需h(x)>0在[0,e]上有解,即-
bx+b-e>0在[0,e]上有解,最后将问题转化为求函数y=-
bx+b-e在[0,e]上的最大值问题即可
(2)先由x1=1,得f′(1)=0,从而f(x)=-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:(1)证明:
⇒f(x)=ax3+bx2=x2(ax+b)
∴f′(x)=3ax2+bx,通过图象可得出,
当x<0时,原函数为减函数,当0<x<x1时,原函数为增函数,当x>x1时,原函数为减函数,
∴当x<0时,导数小于0,当0<x<x1时,导数大于0,当x>x1时,导数小于0,
∴导函数f′(x)=3ax2+bx图象为开口向下的抛物线,且对称轴在0和x1之间
∴a<0,-
>0,∴b>0
(2)解:∵f′(1)=0,∴b=-3a,∴f(x)=-
bx3+bx2
令h(x)=f(x)-g(x)=-
bx3+(b-e)x2=x2(-
bx+b-e)
若在[0,e]上至少存在一点x0,使得f(x0)>g(x0)成立
即h(x)>0在[0,e]上有解,即-
bx+b-e>0在[0,e]上有解
只需y=-
bx+b-e在[0,e]上的最大值大于零,
∵b>0
∴y=-
bx+b-e在[0,e]上的最大值为b-e
∴b>e即可
|
∴f′(x)=3ax2+bx,通过图象可得出,
当x<0时,原函数为减函数,当0<x<x1时,原函数为增函数,当x>x1时,原函数为减函数,
∴当x<0时,导数小于0,当0<x<x1时,导数大于0,当x>x1时,导数小于0,
∴导函数f′(x)=3ax2+bx图象为开口向下的抛物线,且对称轴在0和x1之间
∴a<0,-
| b |
| 6a |
(2)解:∵f′(1)=0,∴b=-3a,∴f(x)=-
| 1 |
| 3 |
令h(x)=f(x)-g(x)=-
| 1 |
| 3 |
| 1 |
| 3 |
若在[0,e]上至少存在一点x0,使得f(x0)>g(x0)成立
即h(x)>0在[0,e]上有解,即-
| 1 |
| 3 |
只需y=-
| 1 |
| 3 |
∵b>0
∴y=-
| 1 |
| 3 |
∴b>e即可
点评:本题考察了导数应用,转化化归的思想方法,解题时要透彻理解函数性质与方程、不等式的内在联系,准确解题

练习册系列答案
相关题目
如图,函数f(x)的图象是曲线OAB,则f(
)的值等于( )
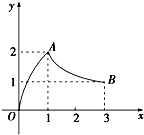
| 1 |
| f(3) |

| A、1 | B、2 | C、3 | D、0 |
 如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( ) 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象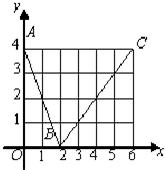 如图,函数f(x)的图象是折线段ABC,其中点A、B、C的坐标分别为(0,4),(2,0),(6,4),若f(x)的值域为[0,4],定义域为[m,n],则|m-n|的最小值为
如图,函数f(x)的图象是折线段ABC,其中点A、B、C的坐标分别为(0,4),(2,0),(6,4),若f(x)的值域为[0,4],定义域为[m,n],则|m-n|的最小值为