题目内容
本小题满分12分)
如图,在棱长为a的正方体ABCD—A1B1C1D1中,E、F分别为棱AB和BC的中点,EF交BD于H。
(1)求二面角B1—EF—B的正切值;
(2)试在棱B1B上找一点M,使D1M⊥平面EFB1,并证明你的结论.
解:(1)连AC、B1H,则EF//AC,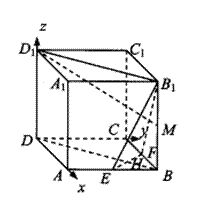
∵AC⊥BD,所以BD⊥EF。
∵B1B⊥平面ABCD,所以B1H⊥EF,
∴∠B1HB为二面角B1—EF—B的平面角。 …………2分
在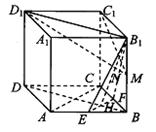
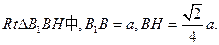
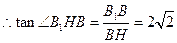
故二面角B1—EF—B的正切值为
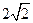
 …………4分
…………4分(2)在棱B1B上取中点M,连D1M、C1M。
∵EF⊥平面B1BDD1,
所以EF⊥D1M。 …………6分
在正方形BB1C1C中,因为M、F分别为BB1、BC的中点,
∴B1F⊥C1M 又因为D1C1⊥平面BCC1B1,所以B1F⊥D1C1,
所以B1F⊥D1M,
∴D1M⊥平面EFB1 …………8分
(3)设D1M与平面EFB1交于点N,则D1N为点D1到平面EFB1的距离。
在Rt△MB1D1中,
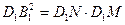 …………10分
…………10分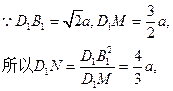
故点D1到平面EFB1的距离为
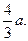 …………12分
…………12分解二:(1)在正方体中,以DA、DC、DD1分别为x、y、z轴建立空间直角坐标系
则
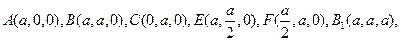
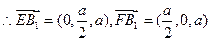 ………………2分
………………2分设平面EFB1的一个法向量为
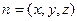
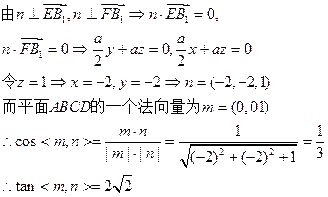
故二面角B1—EF—B的正切值为
 …………6分
…………6分(2)设
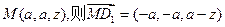
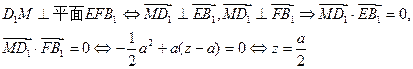
 …………12分
…………12分
解析

练习册系列答案
相关题目
 (2)当
(2)当
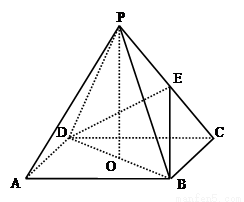
 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.