题目内容
已知函数f(x)=log3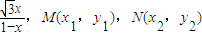 是f(x)图象上的两点,横坐标为
是f(x)图象上的两点,横坐标为 的点P满足2
的点P满足2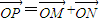 (O为坐标原点).
(O为坐标原点).(Ⅰ)求证:y1+y2为定值;
(Ⅱ)若
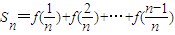 ,其中n∈N*,且n≥2,求Sn;
,其中n∈N*,且n≥2,求Sn;(Ⅲ)已知an=
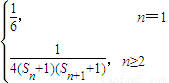 ,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.
,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.
【答案】分析:(1)先用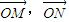 表示出
表示出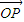 ,再由P是MN的中点可得到x1+x2=1,然后代入到y1+y2=f(x1)+f(x2)结合对数的运算法则即可得到y1+y2=1,得证.
,再由P是MN的中点可得到x1+x2=1,然后代入到y1+y2=f(x1)+f(x2)结合对数的运算法则即可得到y1+y2=1,得证.
(2)先由(Ⅰ)知当x1+x2=1时,y1+y2=1,然后对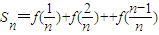 进行倒叙相加即可得到
进行倒叙相加即可得到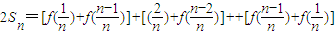 ,再结合x1+x2=1时,y1+y2=1可得到
,再结合x1+x2=1时,y1+y2=1可得到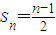 .
.
(3)将(2)中的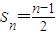 .代入到an的表达式中进行整理当n≥2时满足
.代入到an的表达式中进行整理当n≥2时满足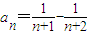 .,然后验证当n=1时满足,再代入到Tn中进行求值,当Tn<m(Sn+1+1)对一切n∈N*都成立时可转化为
.,然后验证当n=1时满足,再代入到Tn中进行求值,当Tn<m(Sn+1+1)对一切n∈N*都成立时可转化为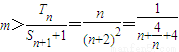 恒成立,再由均值不等式可求出m的范围.
恒成立,再由均值不等式可求出m的范围.
解答:解:(1)由已知可得,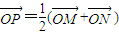 ,
,
∴P是MN的中点,有x1+x2=1.
∴y1+y2=f(x1)+f(x2)
=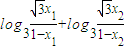
=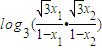
=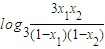
=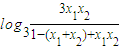
=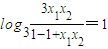 .
.
(2)解:由(Ⅰ)知当x1+x2=1时,y1+y2=f(x1)+f(x1)=1
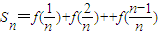 ,
,
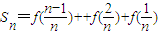 ,
,
相加得
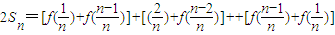
=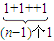
=n-1
∴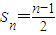 .
.
(3)解:当n≥2时,
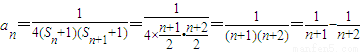 .
.
又当n=1时,
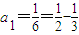 .
.
∴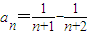 .
.
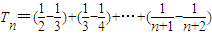 =
=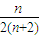 .
.
由于Tn<m(Sn+1+1)对一切n∈N*都成立,
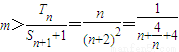
∵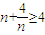 ,当且仅当n=2时,取“=”,
,当且仅当n=2时,取“=”,
∴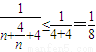
因此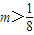 .
.
综上可知,m的取值范围是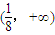 .
.
点评:本题主要考查数列求和的倒叙相加法、数列的裂项法和均值不等式的应用.考查对基础知识的综合运用.
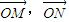 表示出
表示出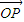 ,再由P是MN的中点可得到x1+x2=1,然后代入到y1+y2=f(x1)+f(x2)结合对数的运算法则即可得到y1+y2=1,得证.
,再由P是MN的中点可得到x1+x2=1,然后代入到y1+y2=f(x1)+f(x2)结合对数的运算法则即可得到y1+y2=1,得证.(2)先由(Ⅰ)知当x1+x2=1时,y1+y2=1,然后对
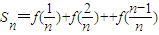 进行倒叙相加即可得到
进行倒叙相加即可得到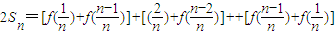 ,再结合x1+x2=1时,y1+y2=1可得到
,再结合x1+x2=1时,y1+y2=1可得到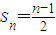 .
.(3)将(2)中的
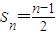 .代入到an的表达式中进行整理当n≥2时满足
.代入到an的表达式中进行整理当n≥2时满足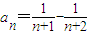 .,然后验证当n=1时满足,再代入到Tn中进行求值,当Tn<m(Sn+1+1)对一切n∈N*都成立时可转化为
.,然后验证当n=1时满足,再代入到Tn中进行求值,当Tn<m(Sn+1+1)对一切n∈N*都成立时可转化为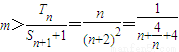 恒成立,再由均值不等式可求出m的范围.
恒成立,再由均值不等式可求出m的范围.解答:解:(1)由已知可得,
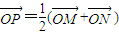 ,
,∴P是MN的中点,有x1+x2=1.
∴y1+y2=f(x1)+f(x2)
=
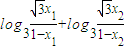
=
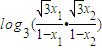
=
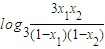
=
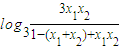
=
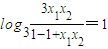 .
.(2)解:由(Ⅰ)知当x1+x2=1时,y1+y2=f(x1)+f(x1)=1
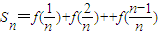 ,
,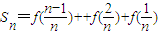 ,
,相加得
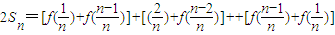
=
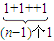
=n-1
∴
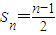 .
.(3)解:当n≥2时,
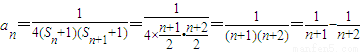 .
.又当n=1时,
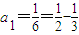 .
.∴
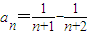 .
.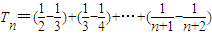 =
=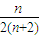 .
.由于Tn<m(Sn+1+1)对一切n∈N*都成立,
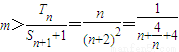
∵
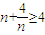 ,当且仅当n=2时,取“=”,
,当且仅当n=2时,取“=”,∴
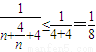
因此
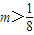 .
.综上可知,m的取值范围是
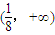 .
.点评:本题主要考查数列求和的倒叙相加法、数列的裂项法和均值不等式的应用.考查对基础知识的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目