题目内容
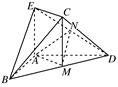
在如图所示的几何体中,四边形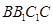 是矩形,
是矩形, 平面
平面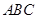 ,
, ,
,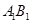 ∥
∥ ,
, ,
,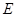 ,
, 分别是
分别是 ,
, 的中点.
的中点.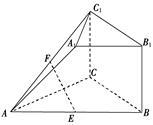
(1)求证: ∥平面
∥平面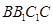 ;
;
(2)求证: 平面
平面 .
.
(1)证明见解析;(2)证明见解析.
解析试题分析:(1)连接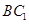 ,应用三角形中位线定理得
,应用三角形中位线定理得 ∥
∥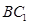 .
.
(2)连结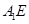 ,
, .可得到平面
.可得到平面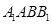
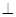 平面
平面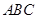 ;
;
通过证明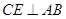 ,得到所以
,得到所以 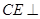 平面
平面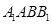 .
.
通过确定四边形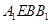 为平行四边形,进一步得到四边形
为平行四边形,进一步得到四边形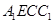 为平行四边形,即可得证.
为平行四边形,即可得证.
试题解析:证明:(1)连接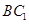 ,因为
,因为 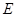 、
、 分别是
分别是 ,
, 的中点,
的中点,
所以  ∥
∥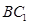 . 2分
. 2分
又因为 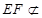 平面
平面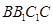 ,
,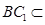 平面
平面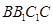 ,
,
所以  ∥平面
∥平面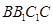 . 4分
. 4分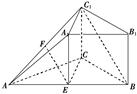
(2)连结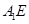 ,
, .因为
.因为  平面
平面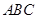 ,
,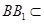 平面
平面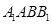 ,
,
所以 平面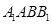
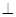 平面
平面 6分
6分
因为  ,
,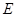 是
是 的中点, 所以
的中点, 所以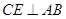
所以 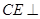 平面
平面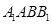 . 8分
. 8分
因为 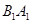 ∥
∥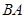 ,
,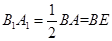
所以 四边形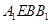 为平行四边形,所以
为平行四边形,所以 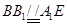 . 10分
. 10分
又 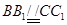 ,所以
,所以 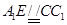 所以 四边形
所以 四边形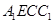 为平行四边形,
为平行四边形,
则 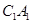 ∥
∥ . 所以
. 所以 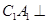 平面
平面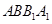 . 12分
. 12分
考点:平行关系,垂直关系.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
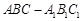 中,侧面
中,侧面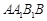 为菱形, 且
为菱形, 且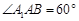 ,
, ,
, 是
是 的中点.
的中点.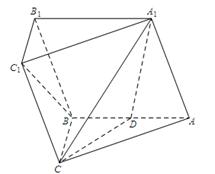
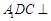 平面
平面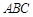 ;
; ∥平面
∥平面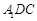 .
. AC,D、E、F分别为线段AC、A1A、C1B的中点.
AC,D、E、F分别为线段AC、A1A、C1B的中点.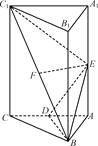


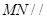 平面
平面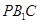 .
. 平面
平面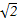 ,E,F分别是BC,AA1的中点.
,E,F分别是BC,AA1的中点.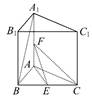
 .
.
 平面
平面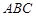 ,四边形
,四边形 为矩形,△
为矩形,△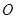 为
为 的中点,
的中点,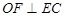 .
.
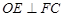 ;
; 的正切值.
的正切值.