题目内容
已知关于x方程xlnx=ax+1（a∈R），下列说法正确的是（ ）A．方程可能没有实数根
B．方程可能有两个实数根
C．方程一定有一个实数根
D．方程一定有两个实数根
【答案】分析：先将方程变形为lnx=a+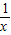
，构造函数f（x）=lnx-a-
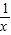，确定函数f（x）=lnx-a-
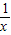在（0，+∞）上单调增，再利用零点存在定理即可得到结论．
解答：解：∵x＞0，∴方程xlnx=ax+1可化为lnx=a+
构造函数f（x）=lnx-a-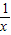
，则f′（x）=
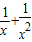＞0
∴函数f（x）=lnx-a-
在（0，+∞）上单调增
∵x→0时，f（x）＜0，x→+∞时，f（x）＞0
∴方程一定有一个实数根
故选C．
点评：本题重点考查方程根的存在性，考查导数知识的运用，解题的关键是构建函数，确定函数的单调性．
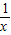，构造函数f（x）=lnx-a-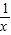，确定函数f（x）=lnx-a-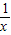在（0，+∞）上单调增，再利用零点存在定理即可得到结论．解答：解：∵x＞0，∴方程xlnx=ax+1可化为lnx=a+
构造函数f（x）=lnx-a-
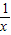，则f′（x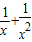）=＞0∴函数f（x）=lnx-a-
在（0，+∞）上单调增∵x→0时，f（x）＜0，x→+∞时，f（x）＞0
∴方程一定有一个实数根
故选C．
点评：本题重点考查方程根的存在性，考查导数知识的运用，解题的关键是构建函数，确定函数的单调性．
练习册系列答案
相关题目