题目内容
已知函数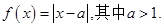
(I)
(II)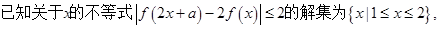
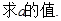
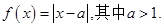
(I)

(II)
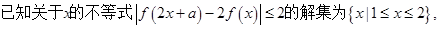
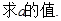
(I)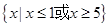 (II)
(II)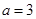
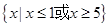 (II)
(II)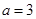
(I)解法一当a=2时,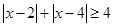 ,利用几何意义可知表示数x到2与4的距离之和大于等于4,又2
,利用几何意义可知表示数x到2与4的距离之和大于等于4,又2
和4之间的距离为2,即数x可以2和4为标准分别向左或者向右移1各单位。故不等式的解集为
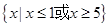 。
。
(I)解法二当a=2时,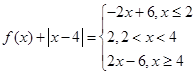
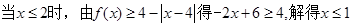
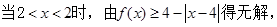
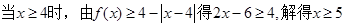
故不等式的解集为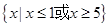 。
。
(II)令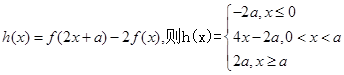
由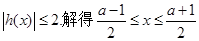 ,又知
,又知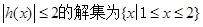
所以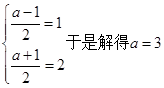
第一问的解法一主要运用了绝对值的几何意义,这种方法比较直观简单,解法二主要运用绝对值的意义进行分类讨论解决;第二问主要是含有字母a,以a作为依据分为三段来解决,最后于所给的解集相等进而求得a的值。
【考点定位】本题考查绝对值不等式以及含有参数不等式的分类讨论。
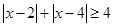 ,利用几何意义可知表示数x到2与4的距离之和大于等于4,又2
,利用几何意义可知表示数x到2与4的距离之和大于等于4,又2和4之间的距离为2,即数x可以2和4为标准分别向左或者向右移1各单位。故不等式的解集为
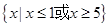 。
。(I)解法二当a=2时,
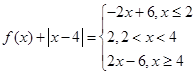
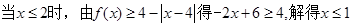
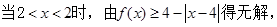
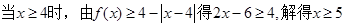
故不等式的解集为
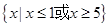 。
。(II)令
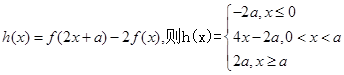
由
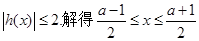 ,又知
,又知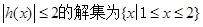
所以
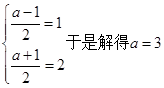
第一问的解法一主要运用了绝对值的几何意义,这种方法比较直观简单,解法二主要运用绝对值的意义进行分类讨论解决;第二问主要是含有字母a,以a作为依据分为三段来解决,最后于所给的解集相等进而求得a的值。
【考点定位】本题考查绝对值不等式以及含有参数不等式的分类讨论。

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 在区间(-∞,+∞)上恒成立,求实数a的取值范围
在区间(-∞,+∞)上恒成立,求实数a的取值范围 的解集为 .
的解集为 .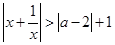 对于一切非零实数
对于一切非零实数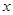 均成立,则实数
均成立,则实数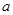 的取值范围是( )
的取值范围是( )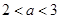
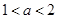
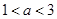
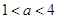
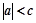
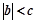 ,求证:
,求证: .
.
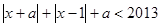 的解集是非空集合,则
的解集是非空集合,则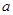 的取值范围是
的取值范围是 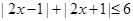 的解集为__________
的解集为__________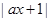 (a∈R),不等式f(x)≤3的解集为{x|?2≤x≤1}.
(a∈R),不等式f(x)≤3的解集为{x|?2≤x≤1}.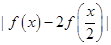 ≤k恒成立,求k的取值范围.
≤k恒成立,求k的取值范围.