题目内容
已知函数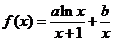 ,曲线
,曲线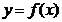 在点
在点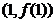 处的切线方程为
处的切线方程为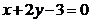 。
。
(Ⅰ)求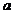 、
、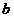 的值;
的值;
(Ⅱ)如果当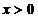 ,且
,且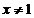 时,
时,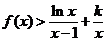 ,求
,求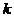 的取值范围。
的取值范围。
【答案】
解析:(Ⅰ)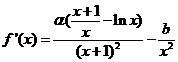
由于直线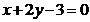 的斜率为
的斜率为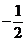 ,且过点
,且过点 ,故
,故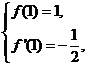 即
即
 解得
解得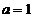 ,
, 。
。
(Ⅱ)由(Ⅰ)知 ,所以
,所以
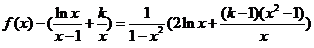 。
。
考虑函数
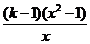
 ,则
,则 。
。
(i)设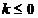 ,由
,由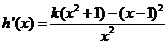 知,当
知,当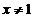 时,
时,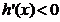 ,h(x)递减。而
,h(x)递减。而 故当
故当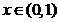 时,
时,
 ,可得
,可得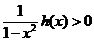 ;
;
当x (1,+
(1,+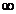 )时,h(x)<0,可得
)时,h(x)<0,可得 h(x)>0
h(x)>0
从而当x>0,且x 1时,f(x)-(
1时,f(x)-(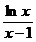 +
+ )>0,即f(x)>
)>0,即f(x)>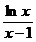 +
+ .
.
 (ii)设0<k<1.由于
(ii)设0<k<1.由于 =
=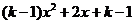 的图像开口向下,且
的图像开口向下,且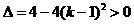 ,对称轴x=
,对称轴x= .当x
.当x (1,
(1,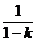 )时,(k-1)(x2 +1)+2x>0,故
)时,(k-1)(x2 +1)+2x>0,故 (x)>0,而h(1)=0,故当x
(x)>0,而h(1)=0,故当x (1,
(1,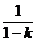 )时,h(x)>0,可得
)时,h(x)>0,可得 h(x)<0,与题设矛盾。
h(x)<0,与题设矛盾。
(iii)设k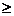 1.此时
1.此时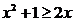 ,
,
 (x)>0,而h(1)=0,故当x
(x)>0,而h(1)=0,故当x (1,+
(1,+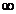 )时,h(x)>0,可得
)时,h(x)>0,可得 h(x)<0,与题设矛盾。
h(x)<0,与题设矛盾。
综合得,k的取值范围为(-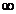 ,0]
,0]
点评;求参数的范围一般用离参法,然后用导数求出最值进行求解。若求导后不易得到极值点,可二次求导,还不行时,就要使用参数讨论法了。即以参数为分类标准,看是否符合题意。求的答案。此题用的便是后者。

练习册系列答案
相关题目
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 ,
, 的值
的值 时,
时,
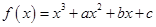 ,曲线
,曲线 在点
在点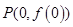 处的切线是
处的切线是 :
:
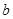 ,
,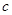 的值;
的值;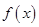 在
在 上单调递增,求
上单调递增,求 的取值范围
的取值范围 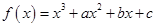 ,曲线
,曲线 在点
在点 处的切线是
处的切线是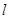 :
: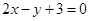
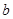 ,
,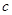 的值;
的值;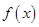 在
在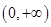 上单调递增,求
上单调递增,求 的取值范围
的取值范围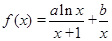 ,曲线
,曲线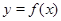 在点
在点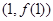 处的切线方程为
处的切线方程为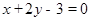 。
。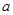 、
、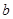 的值;
的值;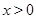 ,且
,且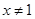 时,
时,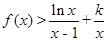 ,求
,求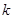 的取值范围
的取值范围