题目内容
(本小题满分12分)已知函数
(1)若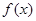 是单调函数,求
是单调函数,求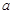 的取值范围;
的取值范围;
(2)若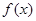 有两个极值点
有两个极值点 ,证明:
,证明: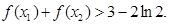
【答案】
解:
(Ⅰ)f(x)=-lnx-ax2+x,
f¢(x)=-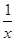 -2ax+1=-
-2ax+1=-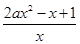 . …2分
. …2分
令Δ=1-8a.
当a≥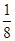 时,Δ≤0,f¢(x)≤0,f(x)在(0,+∞)单调递减. …4分
时,Δ≤0,f¢(x)≤0,f(x)在(0,+∞)单调递减. …4分
当0<a<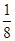 时,Δ>0,方程2ax2-x+1=0有两个不相等的正根x1,x2,
时,Δ>0,方程2ax2-x+1=0有两个不相等的正根x1,x2,
不妨设x1<x2,
则当x∈(0,x1)∪(x2,+∞)时,f¢(x)<0,当x∈(x1,x2)时,f¢(x)>0,
这时f(x)不是单调函数.
综上,a的取值范围是[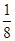 ,+∞). …6分
,+∞). …6分
(Ⅱ)由(Ⅰ)知,当且仅当a∈(0,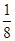 )时,f(x)有极小值点x1和极大值点x2,
)时,f(x)有极小值点x1和极大值点x2,
且x1+x2=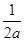 ,x1x2=
,x1x2=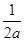 .
.
f(x1)+f(x2)=-lnx1-ax +x1-lnx2-
+x1-lnx2-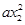 +x2
+x2
=-(lnx1+lnx2)-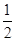 (x1-1)-
(x1-1)-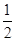 (x2-1)+(x1+x2)
(x2-1)+(x1+x2)
=-ln(x1x2)+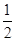 (x1+x2)+1=ln(2a)+
(x1+x2)+1=ln(2a)+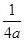 +1. …9分
+1. …9分
令g(a)=ln(2a)+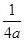 +1,a∈(0,
+1,a∈(0,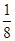 ],
],
则当a∈(0,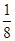 )时,g¢(a)=
)时,g¢(a)=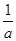 -
-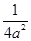 =
=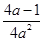 <0,g(a)在(0,
<0,g(a)在(0,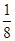 )单调递减,
)单调递减,
所以g(a)>g(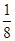 )=3-2ln2,即f(x1)+f(x2)>3-2ln2. …12分
)=3-2ln2,即f(x1)+f(x2)>3-2ln2. …12分
【解析】本题考查函数的单调性和不等式的证明,考查学生利用求导研究函数性质的解题能力和分类讨论思想的应用。第一问借助函数为单调函数进行转化;第二问通过构造函数,证明函数的单调性分析得到函数的最值达到证明不等式的目的.

练习册系列答案
相关题目