题目内容
已知点P为抛物线y2=2x上的动点,点P在y轴上的射影为M,点A的坐标为 ,则|PA|+|PM|的最小值是 .
,则|PA|+|PM|的最小值是 .
【答案】分析:先根据抛物线的方程求得焦点坐标和准线方程,延长PM交准线于H点,由抛物线的定义可得|PF|=|PH|,故|PM|+|PA|
=|PF|+|PA|- ,由|PF|+|PA|≥|FA|可得所求的最小值为|FA|-
,由|PF|+|PA|≥|FA|可得所求的最小值为|FA|- .利用两点间的距离公式求得|FA|,即可得到|最小值|FA|-
.利用两点间的距离公式求得|FA|,即可得到|最小值|FA|- 的值.
的值.
解答:解:解:依题意可知焦点F( ,0),准线 x=-
,0),准线 x=- ,延长PM交准线于H点,则由抛物线的定义可得|PF|=|PH|,
,延长PM交准线于H点,则由抛物线的定义可得|PF|=|PH|,
∴|PM|=|PH|- =|PF|-
=|PF|- .
.
∴|PM|+|PA|=|PF|+|PA|- ,我们只有求出|PF|+|PA|最小值即可.
,我们只有求出|PF|+|PA|最小值即可.
由三角形两边长大于第三边可知,|PF|+|PA|≥|FA|,
当点P是线段FA和抛物线的交点时,|PF|+|PA|可取得最小值为|FA|,利用两点间的距离公式求得|FA|=5.
则所求为|PM|+|PA|=5- =
= .
.
故答案为: .
.
点评:本题主要考查了抛物线的定义和简单性质,考查了考生分析问题的能力,数形结合的思想的运用.
=|PF|+|PA|-
 ,由|PF|+|PA|≥|FA|可得所求的最小值为|FA|-
,由|PF|+|PA|≥|FA|可得所求的最小值为|FA|- .利用两点间的距离公式求得|FA|,即可得到|最小值|FA|-
.利用两点间的距离公式求得|FA|,即可得到|最小值|FA|- 的值.
的值.解答:解:解:依题意可知焦点F(
 ,0),准线 x=-
,0),准线 x=- ,延长PM交准线于H点,则由抛物线的定义可得|PF|=|PH|,
,延长PM交准线于H点,则由抛物线的定义可得|PF|=|PH|,∴|PM|=|PH|-
 =|PF|-
=|PF|- .
.∴|PM|+|PA|=|PF|+|PA|-
 ,我们只有求出|PF|+|PA|最小值即可.
,我们只有求出|PF|+|PA|最小值即可.由三角形两边长大于第三边可知,|PF|+|PA|≥|FA|,
当点P是线段FA和抛物线的交点时,|PF|+|PA|可取得最小值为|FA|,利用两点间的距离公式求得|FA|=5.
则所求为|PM|+|PA|=5-
 =
= .
.故答案为:
 .
.点评:本题主要考查了抛物线的定义和简单性质,考查了考生分析问题的能力,数形结合的思想的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
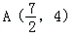 ,则|PA|+|PM|的最小值是( )
,则|PA|+|PM|的最小值是( )