题目内容
已知点P为抛物线y2=2x上的动点,则点P到直线y=x+2的距离的最小值为 .
【答案】分析:求出与直线y=x+2平行且与抛物线y2=2x相切的直线方程,然后由两条平行线间的距离公式求解.
解答: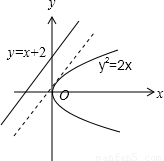 解:如图,
解:如图,
设与直线y=x+2平行的直线方程为y=x+m.
联立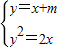 ,得x2+(2m-2)x+m2=0.
,得x2+(2m-2)x+m2=0.
由△=(2m-2)2-4m2=0,得m= .
.
所以与直线y=x+2平行且与抛物线y2=2x相切的直线方程为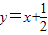 .
.
由两平行线间的距离公式得:d=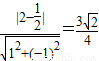 .
.
所以点P到直线y=x+2的距离的最小值为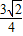 .
.
故答案为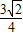 .
.
点评:本题考查了直线与圆锥曲线的关系,考查了数学转化思想方法,训练了两条平行线间的距离的求法,是中档题.
解答:
 解:如图,
解:如图,设与直线y=x+2平行的直线方程为y=x+m.
联立
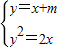 ,得x2+(2m-2)x+m2=0.
,得x2+(2m-2)x+m2=0.由△=(2m-2)2-4m2=0,得m=
 .
.所以与直线y=x+2平行且与抛物线y2=2x相切的直线方程为
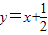 .
.由两平行线间的距离公式得:d=
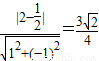 .
.所以点P到直线y=x+2的距离的最小值为
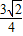 .
.故答案为
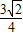 .
.点评:本题考查了直线与圆锥曲线的关系,考查了数学转化思想方法,训练了两条平行线间的距离的求法,是中档题.

练习册系列答案
相关题目
 ,则|PA|+|PM|的最小值是 .
,则|PA|+|PM|的最小值是 .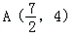 ,则|PA|+|PM|的最小值是( )
,则|PA|+|PM|的最小值是( )