题目内容
如果对于任意一个三角形,只要它的三边长 都在函数
都在函数 的定义域内,则
的定义域内,则  也是某个三角形的三边长,则称函数
也是某个三角形的三边长,则称函数 为“保三角形函数”.现有下列五个函数: ①
为“保三角形函数”.现有下列五个函数: ① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.
则其中是 “保三角形函数”的有 .(写出所有正确的序号)
 都在函数
都在函数 的定义域内,则
的定义域内,则  也是某个三角形的三边长,则称函数
也是某个三角形的三边长,则称函数 为“保三角形函数”.现有下列五个函数: ①
为“保三角形函数”.现有下列五个函数: ① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.则其中是 “保三角形函数”的有 .(写出所有正确的序号)
①④
试题分析:满足三角形的条件是两边之和大于第三边,两边之差小于第三边。
因为
 是单调函数,且是自变量x的2倍,所以当三边长
是单调函数,且是自变量x的2倍,所以当三边长 都在函数
都在函数 的定义域内,2a,2b,2c,也极值函数定义域内,且满足构成三角形的条件,所以①是;
的定义域内,2a,2b,2c,也极值函数定义域内,且满足构成三角形的条件,所以①是;②中,当三边长
 都在函数
都在函数 的定义域内,而
的定义域内,而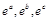 虽在函数定义域内,由于函数为增函数,且增大幅度的不同,不一定满足构成三角形的条件,所以不是。
虽在函数定义域内,由于函数为增函数,且增大幅度的不同,不一定满足构成三角形的条件,所以不是。③中取
 分别为3,4,5,则函数值分别为9,16,25,不能构成三角形,不是
分别为3,4,5,则函数值分别为9,16,25,不能构成三角形,不是④f(x)= 是保三角形函数.
对任意一个三角形的三边长a,b,c,则a+b>c,b+c>a,c+a>b,
f(a)= ,f(b)= ,f(c)= .
因为(+)2=a+2+b>c+2>()2,所以+>.
同理可以证明:+>,+>.
所以f(a)、f(b)、f(c)也是某个三角形的三边长,故 f(x)= 是保三角形函数.
⑤
 在定义域内不单调,很明显看出来,不是。综上知是“保三角形函数”的有①④。
在定义域内不单调,很明显看出来,不是。综上知是“保三角形函数”的有①④。点评:难题,本题是新定义问题,作为填空题,可以通过举反例排除,集合函数图象“猜测”判断。作为解析该题,则为难题。

练习册系列答案
相关题目
 是
是 上单调递增
上单调递增 上单调递增
上单调递增  ,则
,则 ( )
( ) ,
, ]上是减函数
]上是减函数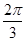 ,
, ]上是增函数
]上是增函数 ,
, ]上是增函数
]上是增函数 ,
, ]上是减函数
]上是减函数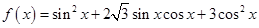 .
.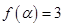 ,且
,且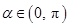 ,求
,求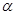 的值;
的值;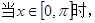 求函数
求函数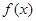 的单调递增区间;
的单调递增区间;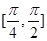 ,不等式
,不等式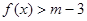 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
 的图象如图所示,则
的图象如图所示,则 等于
等于




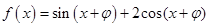 是奇函数,则
是奇函数,则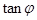 = .
= . 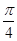 )的单调减区间为( )
)的单调减区间为( )



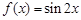 ,则
,则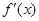 等于
等于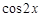
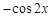

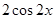
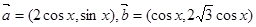 ,函数
,函数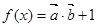 .
.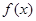 的单调递增区间;
的单调递增区间;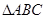 中,
中,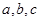 分别是角
分别是角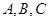 的对边,
的对边,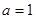 且
且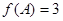 ,求
,求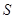 的最大值.
的最大值.