题目内容
已知:x>-1,求x-1+
的最小值是
| 4 | x+1 |
2
2
.分析:由已知中x>-1,可得x+1>0,将原式x-1+
化为x+1+
-2后,利用基本不等式,易求出x-1+
的最小值.
| 4 |
| x+1 |
| 4 |
| x+1 |
| 4 |
| x+1 |
解答:解:∵x>-1
∴x+1>0
∴x-1+
=x+1+
-2≥2
-2=4-2=2
故答案为:2
∴x+1>0
∴x-1+
| 4 |
| x+1 |
| 4 |
| x+1 |
(x+1)
|
故答案为:2
点评:本题考查的知识点是基本不等式在最值问题中的应用,其中根据已知判断出x+1>0,并将x-1+
化为x+1+
-2,为基本不等式的使用创造出“一正,二定”的前提条件是解答本题的关键.
| 4 |
| x+1 |
| 4 |
| x+1 |

练习册系列答案
相关题目
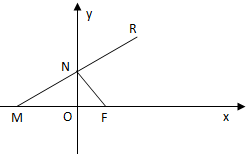 (2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且
(2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且