题目内容
如图,在△ABC中,D是BC边上的任一点(D与B,C不重合),且|
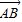 |2=|
|2=|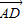 |2+|
|2+|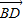 |•|
|•|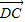 |,试建立适当的直角坐标系,证明:△ABC为等腰三角形.
|,试建立适当的直角坐标系,证明:△ABC为等腰三角形.
【答案】分析:根据三角形的特点以一个顶点为原点,以一条边为坐标轴建立直角坐标系,由条件求出各点的坐标,代入向量的式子,根据向量模的运算进行化简,在求出三角形的边长,即证出结论.
解答: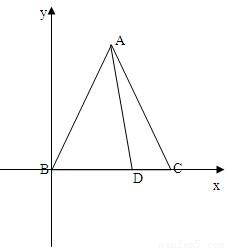 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,
则B(0,0),C(c,0),A(a,b),
D(x,0)(0<x<c)
∴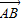 =(-a,-b),
=(-a,-b),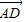 =(x-a,-b),
=(x-a,-b),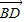 =(x,0),
=(x,0),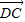 =(c-x,0),
=(c-x,0),
∵|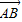 |2=|
|2=|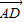 |2+|
|2+|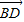 |•|
|•|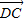 |
|
∴a2+b2=(a-x)2+b2+x•(c-x)
∴a2+b2=a2+x2-2ax+cx-x2,
∴2ax=cx
∵0<x<c,∴2a=c,
∴|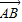 |=a2+b2,|
|=a2+b2,|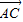 |=(a-c)2+b2=a2+b2=|
|=(a-c)2+b2=a2+b2=|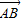 |,
|,
∴△ABC为等腰三角形.
点评:本题考查了利用向量的数量积运算以及向量的坐标运算求向量的模,主要建立坐标系利用图形中的垂直条件,尽量把点放在坐标轴上.
解答:
 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,则B(0,0),C(c,0),A(a,b),
D(x,0)(0<x<c)
∴
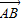 =(-a,-b),
=(-a,-b),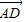 =(x-a,-b),
=(x-a,-b),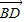 =(x,0),
=(x,0),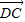 =(c-x,0),
=(c-x,0),∵|
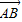 |2=|
|2=|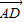 |2+|
|2+|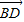 |•|
|•|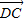 |
|∴a2+b2=(a-x)2+b2+x•(c-x)
∴a2+b2=a2+x2-2ax+cx-x2,
∴2ax=cx
∵0<x<c,∴2a=c,
∴|
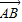 |=a2+b2,|
|=a2+b2,|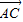 |=(a-c)2+b2=a2+b2=|
|=(a-c)2+b2=a2+b2=|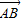 |,
|,∴△ABC为等腰三角形.
点评:本题考查了利用向量的数量积运算以及向量的坐标运算求向量的模,主要建立坐标系利用图形中的垂直条件,尽量把点放在坐标轴上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知