��Ŀ����
���ģ���֪��P1��a1��b1����P2��a2��b2��������Pn��an��bn����nΪ�����������ں���y=ax��a��0��a��1����ͼ���ϣ�����{an}����1Ϊ���2Ϊ����ĵȲ����У���1��������{an}��ͨ�ʽ����֤������{bn}�ǵȱ����У�
��2��������{bn}��ǰn��ĺ�Sn����
| lim |
| n���� |
| Sn |
| Sn+1 |
��3����Qn��an��0������a=
| 2 |
| 3 |
��������1��ֱ�����ö��弴��������{an}��ͨ�ʽ���ٴ����������{bn}��ͨ�ʽ���ö��弴��֤������{bn}�ǵȱ����У�
��2����ֱ�Ӵ��빫ʽ���Sn�Լ�
�ı���ʽ���ٷ�a�IJ�ͬȡֵ������ۼ��ɣ�
��3�����ҵ���OPnQn������ı���ʽ�������Ӧ���У������������������ķ��������OPnQn����������ֵ���ɣ�
��2����ֱ�Ӵ��빫ʽ���Sn�Լ�
| sn |
| sn+1 |
��3�����ҵ���OPnQn������ı���ʽ�������Ӧ���У������������������ķ��������OPnQn����������ֵ���ɣ�
����⣺��1��an=2n-1����n��N*����bn=aan=a2n-1��
��
=a2(��ֵ)��
������{bn}�ǵȱ����У�
��2����Ϊ{bn}�ǵȱ����У��ҹ���a2��1��
��Sn=
��
=
��
��0��a��1ʱ��
=1��
��a��1ʱ��
=
=
=
��
��ˣ�
=
��
��3��bn=(
)2n-1��S��=
•(2n-1)•(
)2n-1��
��cn=
•(2n-1)•(
)2n-1��
��cn���ʱ����
��
���
��n��N*����n=2��
����n=2ʱcnȡ�����ֵ
��
��ˡ�OPnQn������������ֵ
��
��
| bn+1 |
| bn |
������{bn}�ǵȱ����У�
��2����Ϊ{bn}�ǵȱ����У��ҹ���a2��1��
��Sn=
| a(1-a2n) |
| 1-a2 |
| Sn |
| Sn+1 |
| 1-a2n |
| 1-a2n+2 |
��0��a��1ʱ��
| lim |
| n���� |
| Sn |
| Sn+1 |
��a��1ʱ��
| lim |
| n���� |
| Sn |
| Sn+1 |
| lim |
| n���� |
| 1-a2n |
| 1-a2n+2 |
| lim |
| n���� |
| ||
|
| 1 |
| a2 |
��ˣ�
| lim |
| n���� |
| Sn |
| Sn+1 |
|
��3��bn=(
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
��cn=
| 1 |
| 2 |
| 2 |
| 3 |
��cn���ʱ����
|
���
|
����n=2ʱcnȡ�����ֵ
| 4 |
| 9 |
��ˡ�OPnQn������������ֵ
| 4 |
| 9 |
���������⿼��Ȳ�������ȱ����еĻ���֪ʶ�����������������еļ��ޣ�֪ʶ��϶࣬�����е��⣮

��ϰ��ϵ�д�
�����Ŀ
 ��
�� ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�
ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�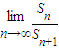 ��
�� ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�
ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ� ��
�� ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�
ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�