题目内容
(文)已知点P1(a1,b1),P2(a2,b2),…,Pn(an,bn)(n为正整数)都在函数y=ax(a>0,a≠1)的图象上,其中{an}是以1为首项,2为公差的等差数列.(1)求数列{an}的通项公式,并证明数列{bn}是等比数列;
(2)设数列{bn}的前n项的和Sn,求
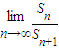 ;
;(3)设Qn(an,0),当
 时,问△OPnQn的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
时,问△OPnQn的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
【答案】分析:(1)直接利用定义即可求数列{an}的通项公式,再代入求出数列{bn}的通项公式,用定义即可证明数列{bn}是等比数列;
(2)先直接代入公式求出Sn以及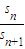 的表达式,再分a的不同取值来求结论即可;
的表达式,再分a的不同取值来求结论即可;
(3)先找到△OPnQn的面积的表达式,设出对应数列,再利用求数列最大项的方法求出△OPnQn的面积的最大值即可.
解答:解:(1)an=2n-1,(n∈N*),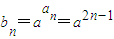 ,
,
∴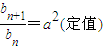 ,
,
∴数列{bn}是等比数列.
(2)因为{bn}是等比数列,且公比a2≠1,
∴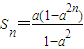 ,
,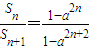 .
.
当0<a<1时,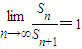 ;
;
当a>1时,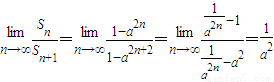 .
.
因此,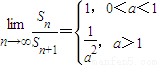 .
.
(3)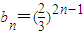 ,
,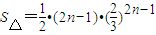 ,
,
设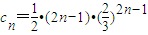 ,
,
当cn最大时,则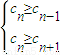 ,
,
解得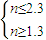 ,n∈N*,∴n=2.
,n∈N*,∴n=2.
所以n=2时cn取得最大值 ,
,
因此△OPnQn的面积存在最大值 .
.
点评:本题考查等差数列与等比数列的基础知识,数列最大项的求法和数列的极限.知识点较多,属于中档题.
(2)先直接代入公式求出Sn以及
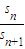 的表达式,再分a的不同取值来求结论即可;
的表达式,再分a的不同取值来求结论即可;(3)先找到△OPnQn的面积的表达式,设出对应数列,再利用求数列最大项的方法求出△OPnQn的面积的最大值即可.
解答:解:(1)an=2n-1,(n∈N*),
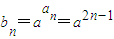 ,
,∴
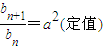 ,
,∴数列{bn}是等比数列.
(2)因为{bn}是等比数列,且公比a2≠1,
∴
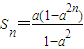 ,
,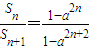 .
.当0<a<1时,
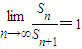 ;
;当a>1时,
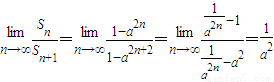 .
.因此,
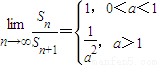 .
.(3)
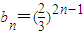 ,
,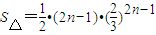 ,
,设
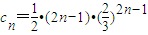 ,
,当cn最大时,则
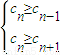 ,
,解得
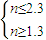 ,n∈N*,∴n=2.
,n∈N*,∴n=2.所以n=2时cn取得最大值
 ,
,因此△OPnQn的面积存在最大值
 .
.点评:本题考查等差数列与等比数列的基础知识,数列最大项的求法和数列的极限.知识点较多,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 ;
; 时,问△OPnQn的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
时,问△OPnQn的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由. ;
; 时,问△OPnQn的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
时,问△OPnQn的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.